Lesson 3. Stacks and Queues
Lesson Objective
- Be familiar with the concept and uses of a stack.
- Be able to describe the creation and maintenance of data within a stack.
- Be able to describe and apply the following operations: push, pop, peek (or top), test for empty stack, test for full stack.
- Be familiar with the concept and uses of a queue.
- Describe the creation and maintenance of data within a queue (linear, circular, priority).
- Describe and apply the following to a linear, circular and priority queue.
- add an item.
- remove an item.
- test for an empty queue.
- test for a full queue.
Lesson Notes
Stack Data Structure
Imagine a stack of textbooks. New books are always placed on top, and when you need a book, you take the one from the top as well. This follows a "Last In, First Out" (LIFO) principle. Essentially, a stack is a data structure that allows for two primary operations: adding an item to the top, removing an item from the top, and checking if the stack is full or empty.
These methods could be written to implement the required functionality of a stack:
- push(item) – adds item to the top of the stack
- pop() – removes and returns the item on the top of the stack
- isFull() – checks if the stack is full
- isEmpty() – checks if the stack is empty
You might also want to write methods to:
- peek() – return the top item without removing it
- size() – return the number of items on the stack
Stack Implementation - Array
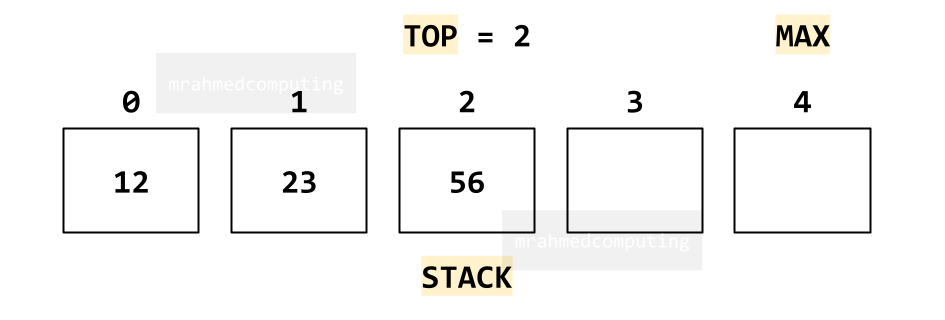
A stack can be effectively implemented using an array. The key to this implementation lies in three variables:
- STACK: This is the array itself, where elements will be stored.
- TOP: This variable points to the index of the array where the top element of the stack is currently located. It essentially acts as a marker for the stack's boundary.
- MAX: This constant defines the maximum number of elements the stack can hold, setting a limit to the array's size.
By utilizing these variables, we can simulate the LIFO (Last In, First Out) behavior of a stack. When an element is added (pushed) to the stack, it's placed at the index indicated by TOP, and then TOP is incremented to point to the next available position. Conversely, when an element is removed (popped) from the stack, the element at the index pointed to by TOP is retrieved, and TOP is decremented to reflect the new top of the stack.
To determine if the stack is full or empty, we compare the value of TOP with MAX and -1 respectively. If TOP equals MAX, the stack is full; if TOP equals -1, the stack is empty.
Stack Implementation - Linked Lists
This method uses a dynamic data structure to represent the stack. You don't need to define the max number of elements.
A stack can also be efficiently implemented using a linked list. In this approach, each element of the stack is represented as a node in the linked list. The crucial variable here is:
- TOP: This pointer holds the address of the topmost element in the linked list, which represents the top of the stack.
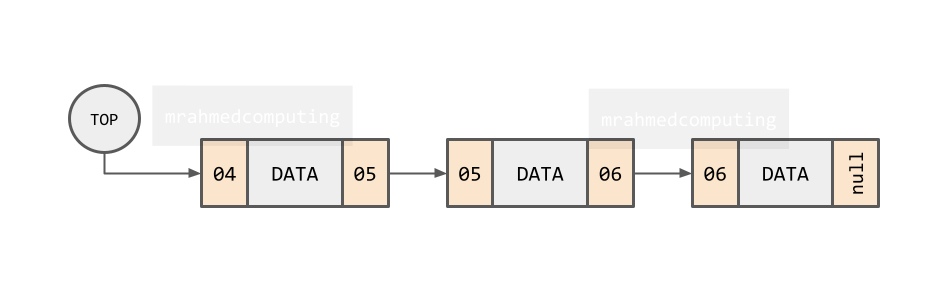
How could it works?
Push operation:
- Create a new node to hold the data to be pushed.
- Set the next pointer of the new node to point to the current TOP.
- Update TOP to point to the new node.
Pop operation:
- If the stack is empty (TOP is null), return an error.
- Store the data of the current TOP node.
- Update TOP to point to the next node in the linked list.
- Return the stored data.
isEmpty operation:
- Check if TOP is null. If it is, the stack is empty.
By using a linked list, the stack can dynamically grow or shrink as needed, unlike an array-based implementation which has a fixed size. This flexibility makes it suitable for scenarios where the number of elements in the stack is unpredictable.
Additionally, linked list implementation often provides better memory efficiency compared to arrays, as it avoids the need for pre-allocating a fixed-size block of memory. This approach maintains the LIFO (Last In, First Out) behavior of a stack while offering the advantages of linked lists in terms of dynamic size and memory management.
Adding to a Stack:
Stack Method - Push
Push is the method used to insert new data elements into a stack.
- Check for free memory. Error if not.
- If full, overflow error and end.
Stack pointer (TOP Variable..(Highlighted greenish blue)) - Shows the top item of the list. Can also point to the next free space in the stack. Depends how you set it up.
| 06 |
|
| 05 |
|
| 04 |
|
| 03 |
D |
| 02 |
C |
| 01 |
B |
| 00 |
A |
- If the stack is not full, increment the pointer (TOP variable in examples) by one.
| 06 |
|
| 05 |
|
| 04 |
|
| 03 |
D |
| 02 |
C |
| 01 |
B |
| 00 |
A |
- Add the data item to the stack where the top pointer is pointing.
| 06 |
|
| 05 |
|
| 04 |
E |
| 03 |
D |
| 02 |
C |
| 01 |
B |
| 00 |
A |
Removing from a Stack:
Stack Method - Pop
The Pop method removes and returns the item on the top of the stack. Pop involves the following steps:
- Check if the stack is empty.
- If empty, underflow error, end.
Stack pointer (TOP Variable..(Highlighted greenish blue)) - Shows the top item of the list. Can also point to the next free space in the stack. Depends how you set it up.
| 06 |
|
| 05 |
|
| 04 |
|
| 03 |
D |
| 02 |
C |
| 01 |
B |
| 00 |
A |
- If not empty, remove the data item specified by the stack pointer.
|
D |
|
... |
| 06 |
|
| 05 |
|
| 04 |
|
| 03 |
|
| 02 |
C |
| 01 |
B |
| 00 |
A |
- Add the data item to the stack where the top pointer is pointing.
|
D |
|
... |
| 06 |
|
| 05 |
|
| 04 |
|
| 03 |
|
| 02 |
C |
| 01 |
B |
| 00 |
A |
Stacks in Java
Java Collection framework provides a Stack class that models and implements a Stack data structure. The class supports one default constructor Stack() which is used to create an empty stack.
Here is an example of a stack data structure applied in Java.
import java.util.Stack;
public class StackExample {
public static void main(String[] args) {
// Create a stack
Stack<Integer> stack = new Stack<>();
// Push elements onto the stack
stack.push(1);
stack.push(2);
stack.push(3);
// Pop elements off the stack
int element1 = stack.pop();
int element2 = stack.pop();
int element3 = stack.pop();
// Print the elements that were popped off the stack
System.out.println(element1); // 3
System.out.println(element2); // 2
System.out.println(element3); // 1
}
}
Stacks in Python 3
Python program to demonstrate stack implementation using a list.
stack = []
# append() function to push element in the stack
stack.append('a')
stack.append('b')
stack.append('c')
print('Initial stack')
print(stack)
# pop() function to pop element from stack in
# LIFO order
print('\nElements popped from stack:')
print(stack.pop())
print(stack.pop())
print(stack.pop())
print('\nStack after elements are popped:')
print(stack)
# uncommenting print(stack.pop()) will cause an
# IndexError as the stack is now empty
Application of Stacks
They are used in a variety of applications, such as:
- Back and forward buttons in web browsers.
- Undo/redo functionality in text editors and image editing software.
- Memory management in computer programming.
- Delimiter checking.
- Implementing recursion in programming.
Web browser example explained:
- The back and forward buttons in a web browser use a stack to store the pages that the user has visited.
- When the user clicks on the back button, the browser pops the previous page off the stack and displays it.
- When the user clicks on the forward button, the browser pushes the current page onto the stack and displays the next page.
Queue Data Structure
A linear data structure that follows the First In First Out (FIFO) principle. This means that the first element added to the queue is the first element removed from the queue.
Here are the basic operations of a queue:
- Enqueue: Add an element to the end of the queue.
- Dequeue: Remove an element from the front of the queue.
- Peek: Get the value of the element at the front of the queue without removing it.
- IsEmpty: Check if the queue is empty.
- IsFull: Check if the queue is full.
Queue Implementation - Array
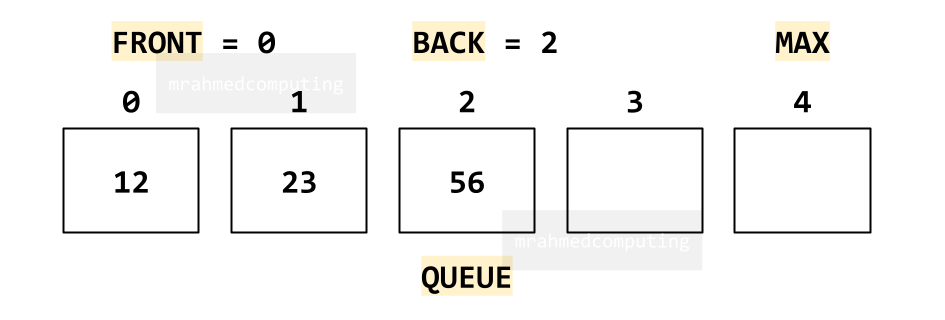
A queue is a First In First Out (FIFO) data structure. We can implement a queue using an array by utilizing the following variables:
- QUEUE: This is the array itself, where elements will be stored.
- FRONT: This index points to the front of the queue, indicating the element to be removed next.
- BACK: This index points to the rear of the queue, indicating where the next element should be inserted.
- MAX: This constant defines the maximum capacity of the queue.
Key operations:
Enqueue (Adding an element):
- Increment the BACK index.
- If BACK exceeds MAX - 1, we've reached the end of the array. To handle this, we can either resize the array or implement a circular queue (where the array is treated as circular).
- Insert the new element at the BACK index of the QUEUE.
Dequeue (Removing an element):
- If the queue is empty (FRONT is equal to BACK), return an error.
- Store the element at the FRONT index.
- Increment the FRONT index.
isEmpty:
- Check if FRONT is equal to BACK. If true, the queue is empty.
isFull:
- Check if BACK is equal to MAX - 1. If true, the queue is full.
By using these variables and operations, we can effectively implement a queue using an array, providing a basic foundation for managing elements in a FIFO order.
Note:
The simple implementation described above can lead to inefficient space utilization as the elements in the queue can become scattered within the array over time. To address this, a circular queue can be implemented by treating the array as circular, where the end connects to the beginning. This allows for better space utilization.
Circular queues are explained later in the lesson/page.
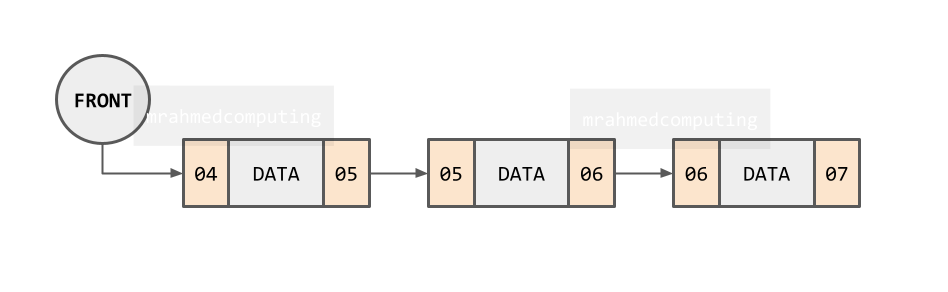
Queue Implementation - Linked List
Queues can be implemented in a variety of ways, but the most common implementation is using a linked list. In a linked list, each element in the queue contains a pointer to the next element in the queue. The front of the queue is simply the first element in the linked list, and the rear of the queue is the last element in the linked list.
Adding to a Queue:
Queue Method - Enqueue()
Enqueue adds an element to the end of the queue. Enqueue does this in the following steps:
- Check if the queue is full..
- If full, return an overflow error and end. If empty, both front and rear pointer would be index 0.
| A |
B |
C |
D |
|
|
|
| 00 |
01 |
02 |
03 |
04 |
05 |
06 |
Front pointer shows the front of the queue. Position 0 (A)
Back pointer shows the last item in the queue. Position 3 (D)
- If the queue is not full, increment the back pointer (BACK variable in examples) by one.
| A |
B |
C |
D |
|
|
|
| 00 |
01 |
02 |
03 |
04 |
05 |
06 |
Front pointer shows the front of the queue. Position 0 (A)
Back pointer shows the last item in the queue. Position 4 (null)
- Add the data item to the queue where the back is pointing.
| A |
B |
C |
D |
E |
|
|
| 00 |
01 |
02 |
03 |
04 |
05 |
06 |
Front pointer shows the front of the queue. Position 0 (A)
Back pointer shows the last item in the queue. Position 4 (E)
Removing from a Queue:
Queue Method - Dequeue()
Dequeue removes an element from the front of the queue. This is done in the following way:
- Check if the queue is empty.
- If empty, return an underflow error and end.
| A |
B |
C |
D |
|
|
|
| 00 |
01 |
02 |
03 |
04 |
05 |
06 |
Front pointer shows the front of the queue. Position 0 (A)
Back pointer shows the last item in the queue. Position 3 (D)
- If not empty, remove the data item specified by the front pointer.
| A |
|
|
B |
C |
D |
|
|
|
|
|
00 |
01 |
02 |
03 |
04 |
05 |
06 |
Front pointer shows the front of the queue. Position 0 (null)
Back pointer shows the last item in the queue. Position 3 (D)
- Increment the front pointer by one.
| A |
|
|
B |
C |
D |
|
|
|
|
|
00 |
01 |
02 |
03 |
04 |
05 |
06 |
Front pointer shows the front of the queue. Position 1 (B)
Back pointer shows the last item in the queue. Position 3 (D)
Checking contents of a Queue:
Queue Method - Peek()
Peek gets the value of the element at the front of the queue without removing it.. Peek does this in the following steps:
- Peek() is initiated.
- Checks if the queue is empty, returns empty if true.
- If not empty, data at the front is accessed using a temporary variable.
| A |
B |
C |
D |
|
|
|
| 00 |
01 |
02 |
03 |
04 |
05 |
06 |
Front pointer shows the front of the queue. Position 0 (A)
Back pointer shows the last item in the queue. Position 3 (D)
Checking if a Queue is full:
Queue Method - isFull()
isFull is used to check if the queue is full. This is done in the following way:
- isFull() is initiated.
- If the back pointer is equal to the MAX, “Full” will be returned.
MAX = 6, BACK = 3, MAX == BACK?
| A |
B |
C |
D |
|
|
|
| 00 |
01 |
02 |
03 |
04 |
05 |
06 |
Front pointer shows the front of the queue. Position 0 (A)
Back pointer shows the last item in the queue. Position 3 (D)
Checking if a Queue is empty:
Queue Method - isEmpty()
isEmpty is used to check if the queue is empty. This is done in the following way:
- isEmpty() is initiated.
- If the front pointer/node is equal to the null, “Empty” will be returned.
| A |
B |
C |
D |
|
|
|
| 00 |
01 |
02 |
03 |
04 |
05 |
06 |
Front pointer shows the front of the queue. Position 0 (A)
Back pointer shows the last item in the queue. Position 3 (D)
FRONT = 0, FRONT == null?
Stacks in Python 3
Python program to demonstrate queue implementation using a list.
# Initializing a queue
queue = []
# Adding elements to the queue
queue.append('a')
queue.append('b')
queue.append('c')
print("Initial queue")
print(queue)
# Removing elements from the queue
print("\nElements dequeued from queue")
print(queue.pop(0))
print(queue.pop(0))
print(queue.pop(0))
print("\nQueue after removing elements")
print(queue)
# Uncommenting print(queue.pop(0)) will raise and IndexError as the queue is now empty
Problems of Queues in Arrays
Problems arise with the implementation of a queue as a fixed-size array.
- How many items can be added? Or removed?
- What happens when the queue is full, but there are some free spaces at the front?
- How could these limitations could be overcome when using an array?
Linear Queues
- Linear data structure.
- Items added to the rear, removed from the front.
- Implemented as an array or linked list.
Simple standard queue structure. As demonstrated in our previous examples.
| A |
B |
C |
D |
|
|
|
| 00 |
01 |
02 |
03 |
04 |
05 |
06 |
Circular Queues
- Variation of linear queue.
- Rear and front ends are connected.
- More efficient use of space.
- Order of operations may change.
Similar to the linear queue, except the last node is connected to the first.
A circular queue algorithm overcomes the problem of reusing the spaces that have been freed by dequeuing from the front of the array.
Ideal if you want to restrict the number of items and have a known memory footprint.
Particularly useful in game design where the number of objects can affect framerate. By spawning up to the limit of the queue.
Note: When the back pointer is in front of the front pointer, it indicates a circular queue.
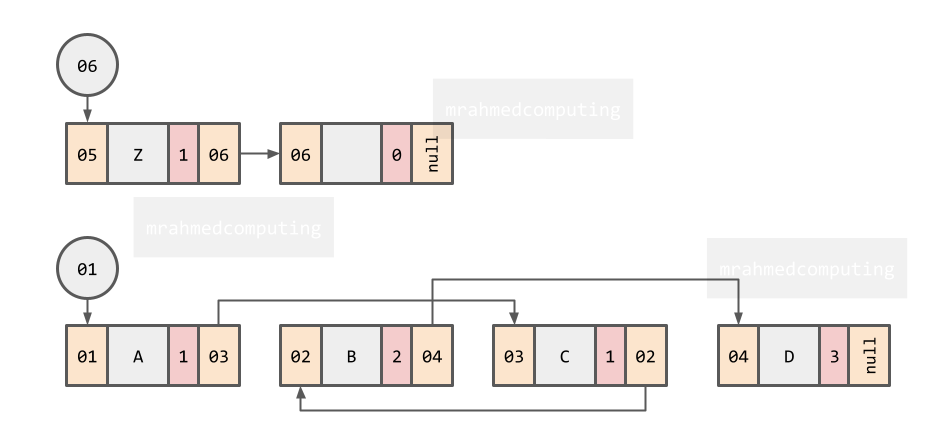
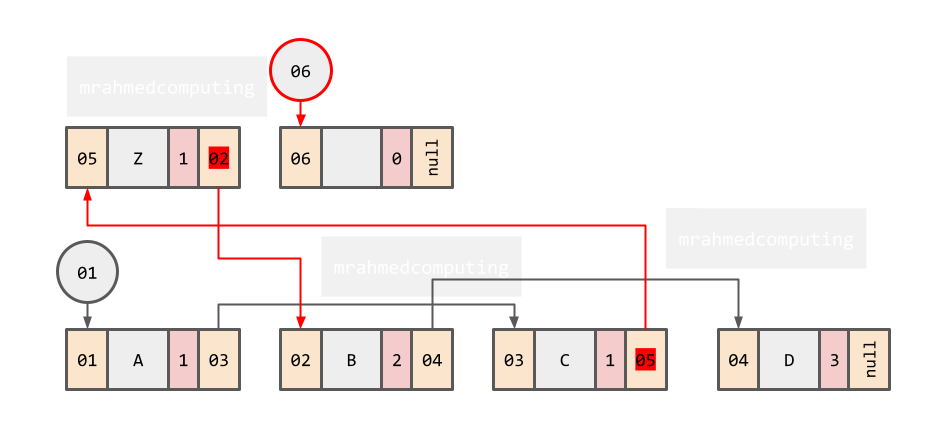
Priority Queues
- Items have a priority.
- New elements inserted ahead of lower priority elements.
- Implemented as a heap or binary search tree.
In a priority queue, some items are allowed to ‘jump’ the queue.
This type of queue is used when the items arriving have some type of priority associated with them.
Items enter the queue in the normal FIFO system, but exit the queue based on the priority.
| RAM |
Address |
Data |
Priority |
Pointer |
| 01 |
A |
1 |
03 |
| 02 |
B |
2 |
04 |
| 03 |
C |
1 |
02 |
| 04 |
D |
3 |
null |
| 05 |
Z |
1 |
06 |
| 06 |
|
0 |
null |
......
| RAM |
Address |
Data |
Priority |
Pointer |
| 01 |
A |
1 |
03 |
| 02 |
B |
2 |
04 |
| 03 |
C |
1 |
05 |
| 04 |
D |
3 |
null |
| 05 |
Z |
1 |
02 |
| 06 |
|
0 |
null |
Applications of Queues
Queues are used in a variety of applications, including:
- Operating systems: Queues are used to manage tasks, such as printing and processing network packets.
- Computer networks: Queues are used to buffer data packets as they are transmitted over a network.
- Web servers: Queues are used to manage incoming requests from web clients.
- Event-driven programming: Queues are used to manage events, such as user input and timer events.
- Printers: page after page etc.
Queues are a versatile and efficient data structure that can be used to solve a wide variety of problems.