Lesson 4. Graphs

Lesson Objective

Be familiar with graphs and their typical.
Be able to explain the terms: graph, weighted graph, unweighted graph, vertex/node, edge/arc, undirected graph, directed graph.
Know how an adjacency matrix and an adjacency list may be used to represent a graph.
Be able to compare the use of adjacency matrices and adjacency lists.
Be able to traverse a graph using a depth first search and a breadth first search.

Lesson Notes

Graph Data Structures

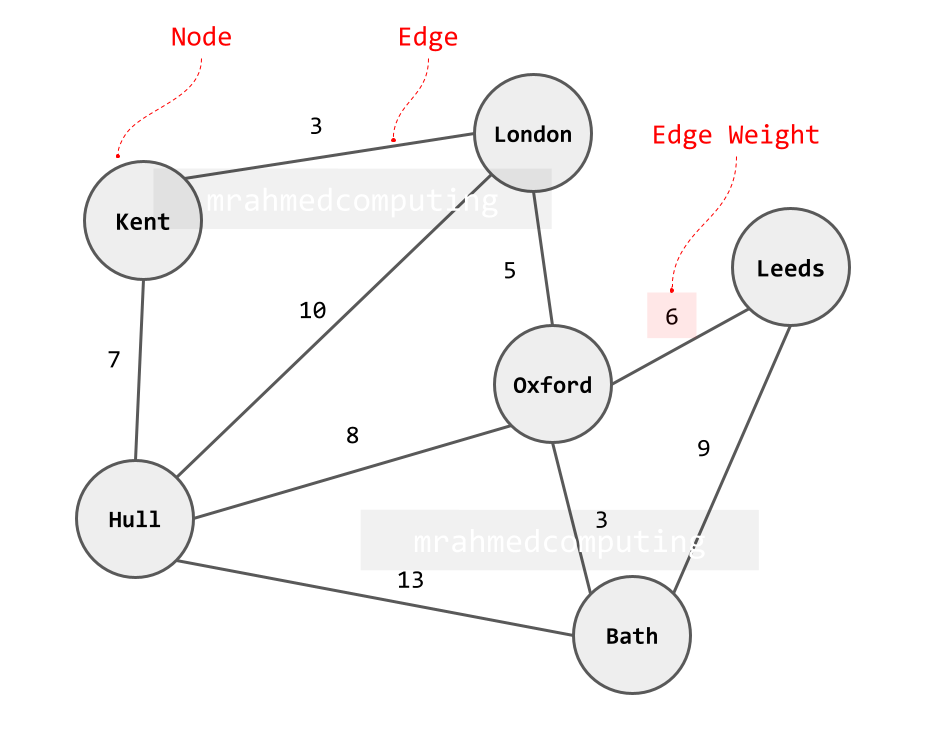
A graph is the name given to an abstract data structure representing complex relationships. It is a non-linear data structure composed of nodes (or vertices) connected by edges.

Key Components of a Graph:

Vertices (Nodes): These represent the individual entities within the graph.
Edges: These connect pairs of vertices, indicating a relationship between them. Edges can be:

Directed: If the relationship has a direction (e.g., following someone on social media).
Undirected: If the relationship is bidirectional (e.g., friendship).
Weighted: If there's a value associated with the edge (e.g., distance between cities).

Common Graph Representations:

Adjacency Matrix: A 2D matrix where rows and columns represent vertices, and the value at a specific position indicates the weight of the edge between the corresponding vertices.
Adjacency List: An array of lists where each index corresponds to a vertex, and the list contains the vertices adjacent to it.

Applications of Graphs:

Graphs are used in a wide range of applications, including:

Social networks
Transportation systems
Routing algorithms
Recommendation systems
Image processing
Network analysis

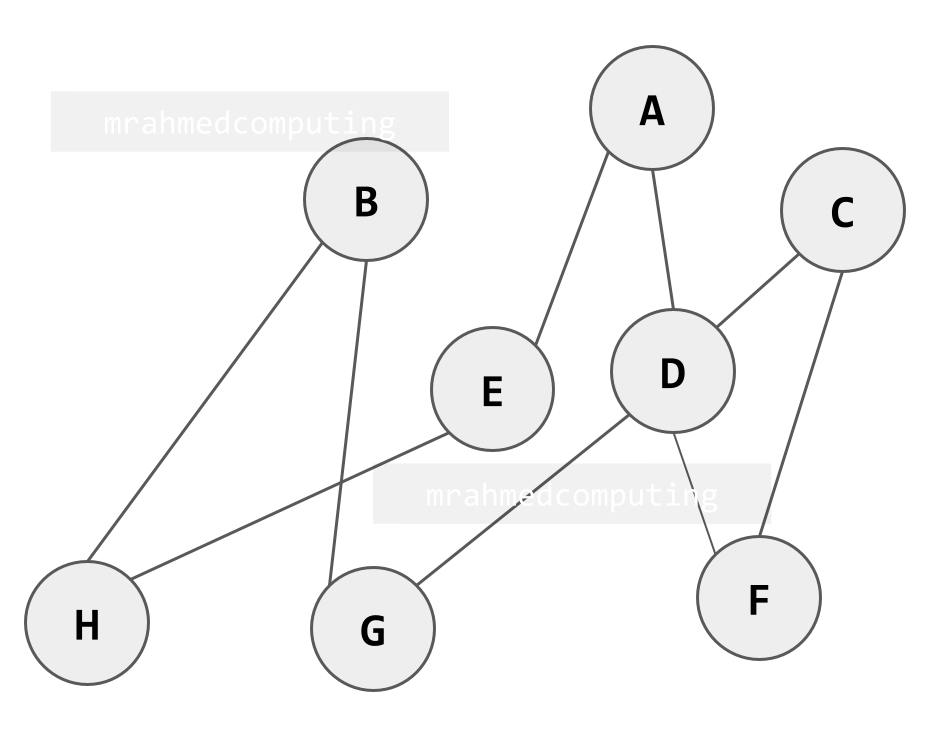
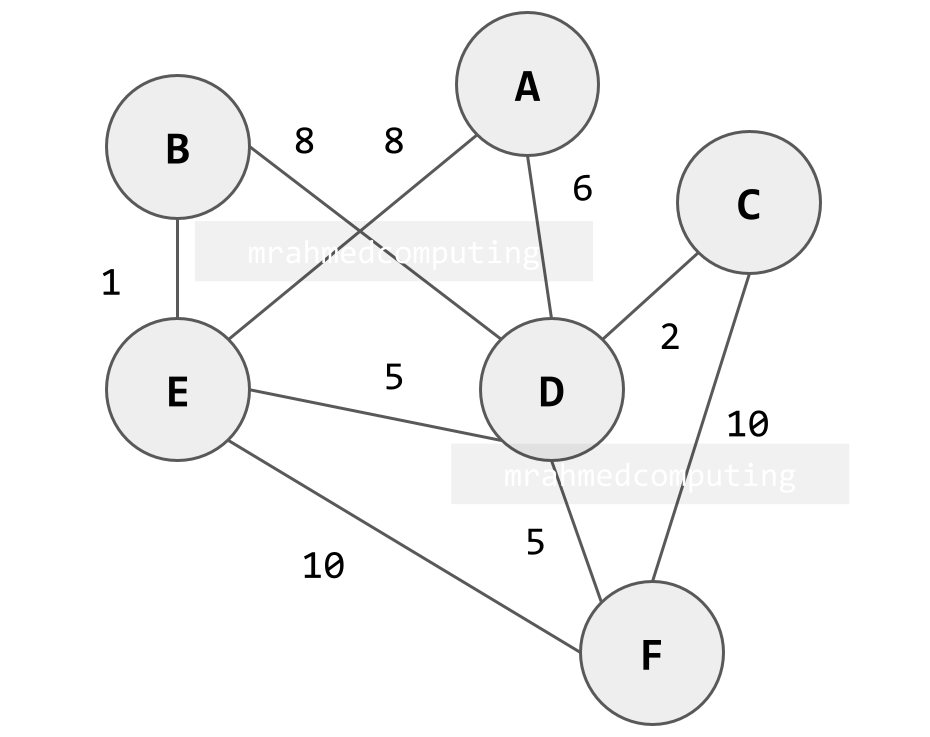
An Undirected Weighted Graph

In this graph is weighted, the weights in the example to the right (or below on mobile devices) represent distances between towns.

It is undirected because there are no arrows on the edges indicating direction.

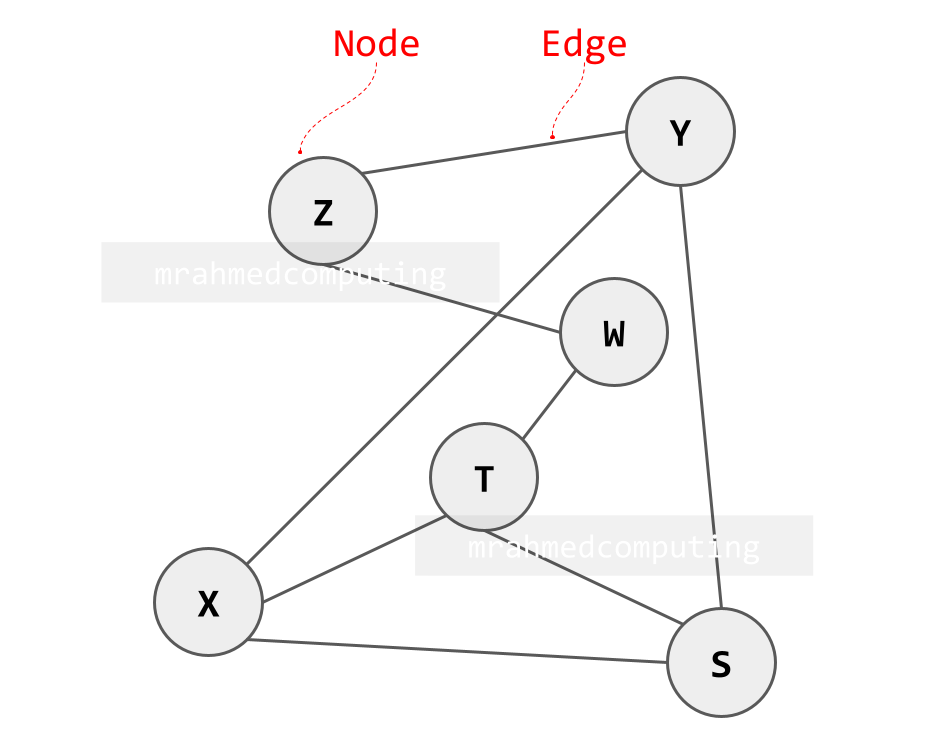
An Undirected (un?)Weighted Graph

In this graph is NOT weighted.

It is undirected because there are no arrows on the edges indicating direction.

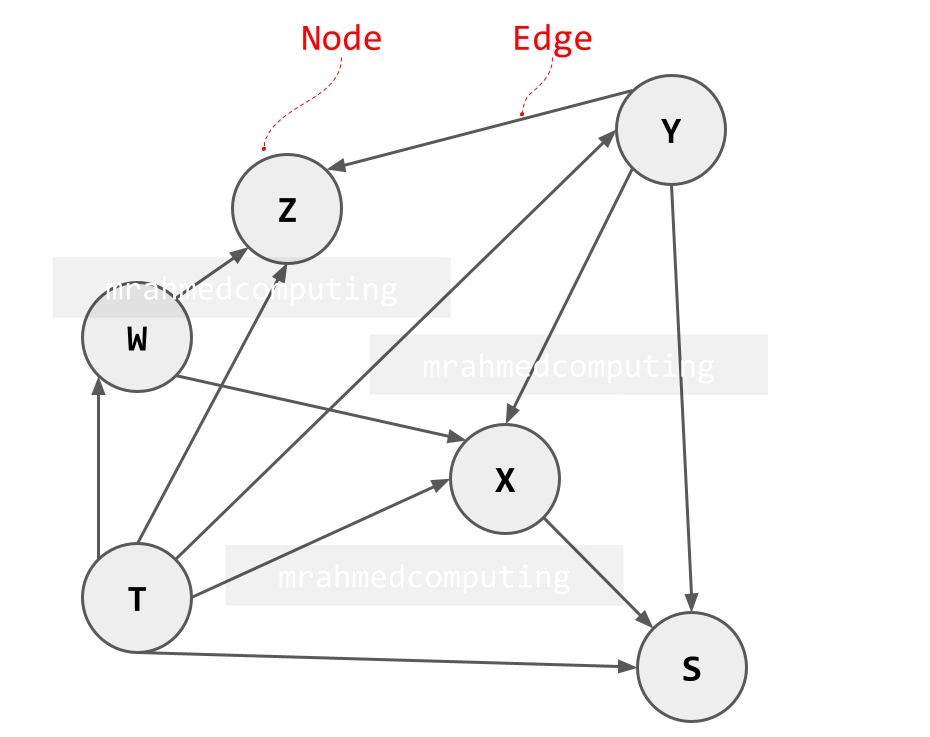
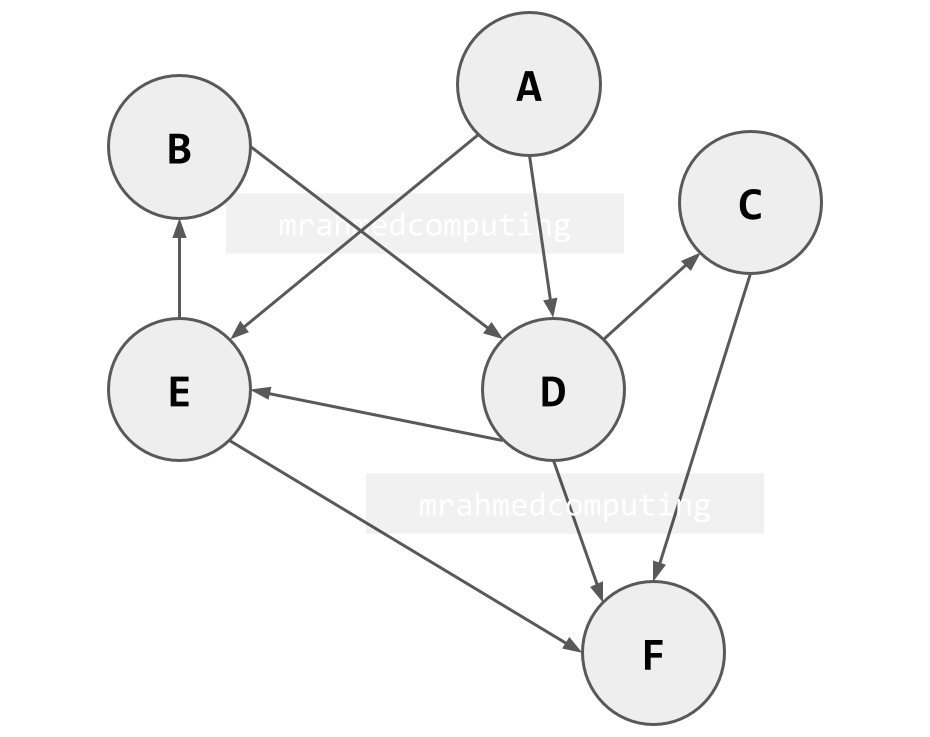
An Directed (un?)Weighted Graph

This graph shows direction (e.g. Y has a link to X, but X does not have a link to Y).

It has no weights associated with the edges.

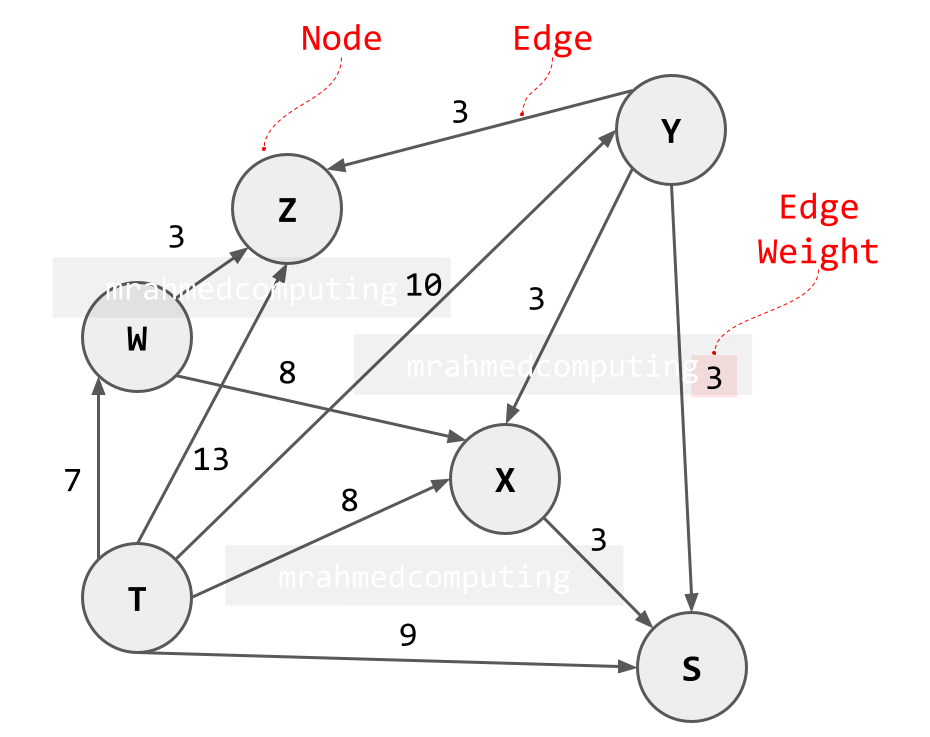
An Directed Weighted Graph

This graph shows direction. However it now has weights associated with the edges.

Graphs - Summary:

A graph is a set of vertices or nodes connected by edges or arcs.
Edges may be weighted, indicating a cost of traversal.
In an undirected graph, all edges are bidirectional.
In a directed graphs, all edges are one-way.
Two nodes are neighbours if they are connected by an edge.
The number of neighbours that a node has is referred to as the degree of a node.

Representing a Graph

A human driver can find their way from one location to another using a map.

A computer needs to represent the information about distances and connections in a structured, numerical way.

Graphs can be implemented using one of two ways:

Adjacency matrix
Adjacency list

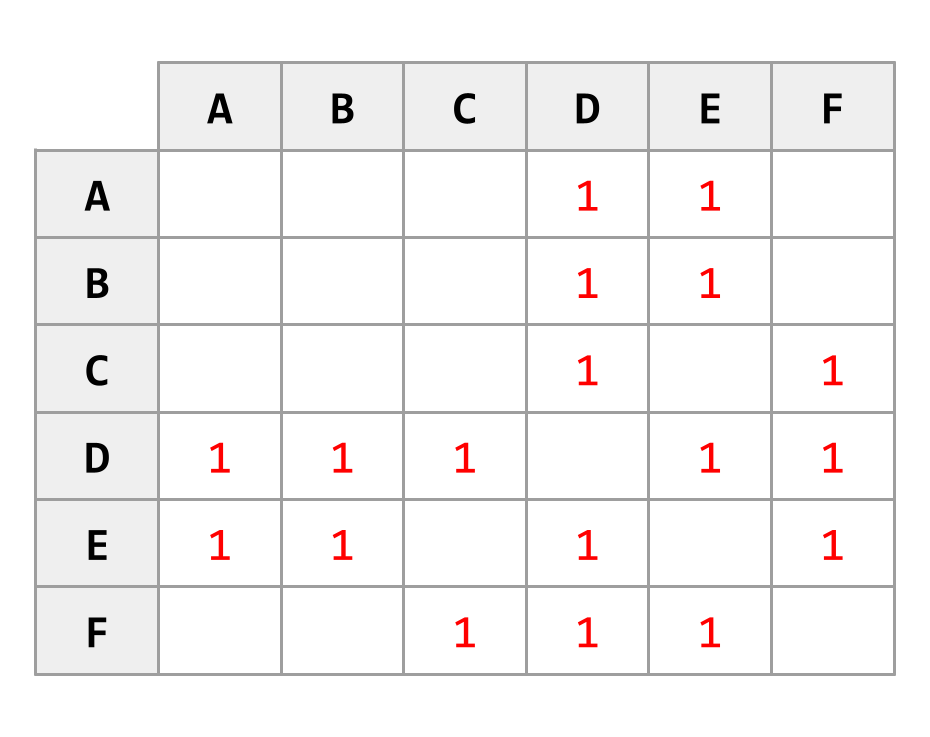
Adjacency Matrix

Each row and column represents a node. The item at [row, column] indicates a connection.

In a unweighted graph, this can be a represented as 1.

Note: Diagram to the right (or below on mobile devices) shows a undirected graph.

In a weighted graph, this can be a represented with the line weight.

Note: Diagram to the right (or below on mobile devices) shows a directed graph.

Matrix Considerations

Advantage: an adjacency matrix is convenient to work with, and adding an edge is simple.
Disadvantage: a sparse graph with not many connections (edges) will leave most of the cells empty, wasting a lot of memory space.

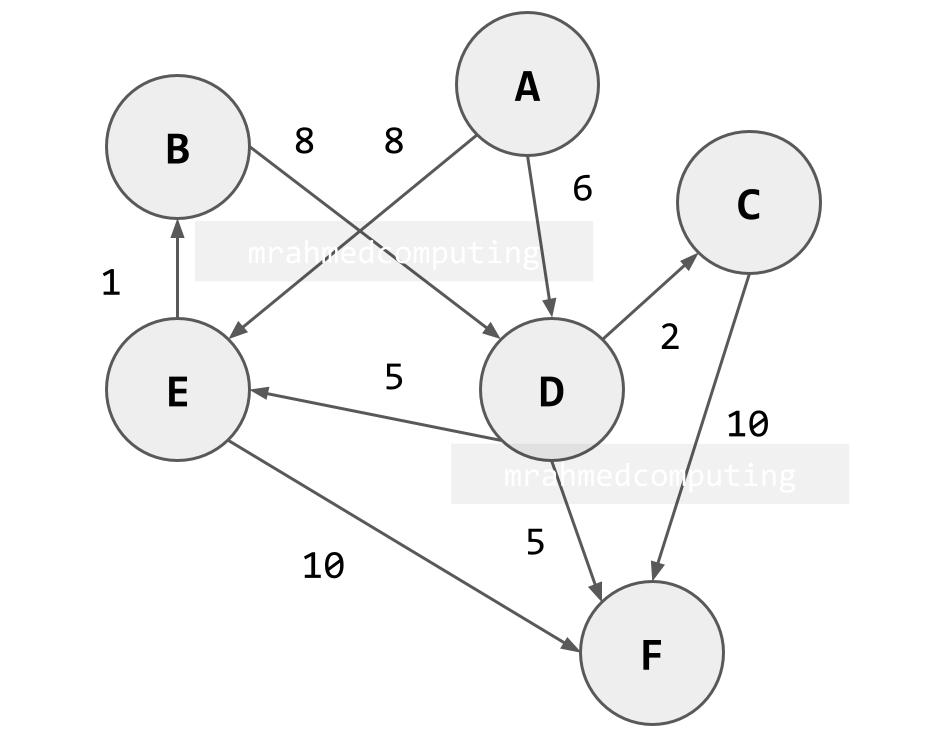
Adjacency List

An adjacency list is an alternative way of representing a graph.

A list of nodes is created, and each node points to a list of adjacent nodes.

Note: Diagram to the right (or below on mobile devices) shows a directed graph.

A weighted graph can be represented as a dictionary of dictionaries, with each key in the dictionary being the node, and the value, a dictionary of adjacent edges and edge weights.

Note: Diagram to the right (or below on mobile devices) shows a undirected graph.

List Considerations

Advantage: It only uses storage for the connections that exist, so it is more space-efficient.
Advantage: It is a good way of representing a large, sparsely connected graph.

Traversing a Graph

You can not supply a single set of predefined steps to insert or remove a node. It depends on the graph and the situation.

Efficient algorithms are needed to traverse a graph to find specific nodes.

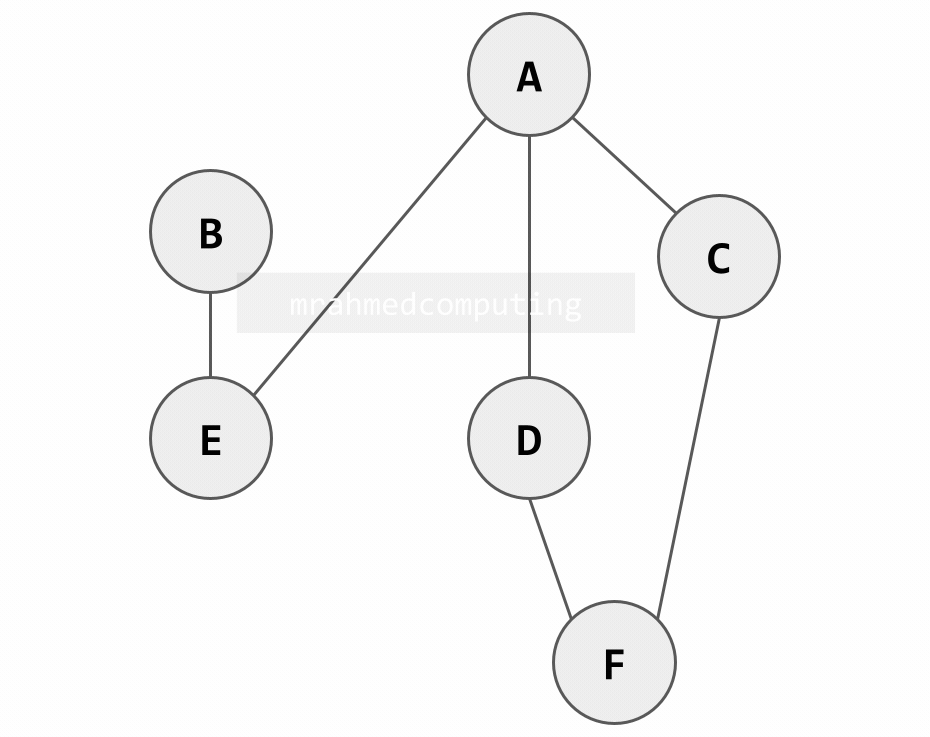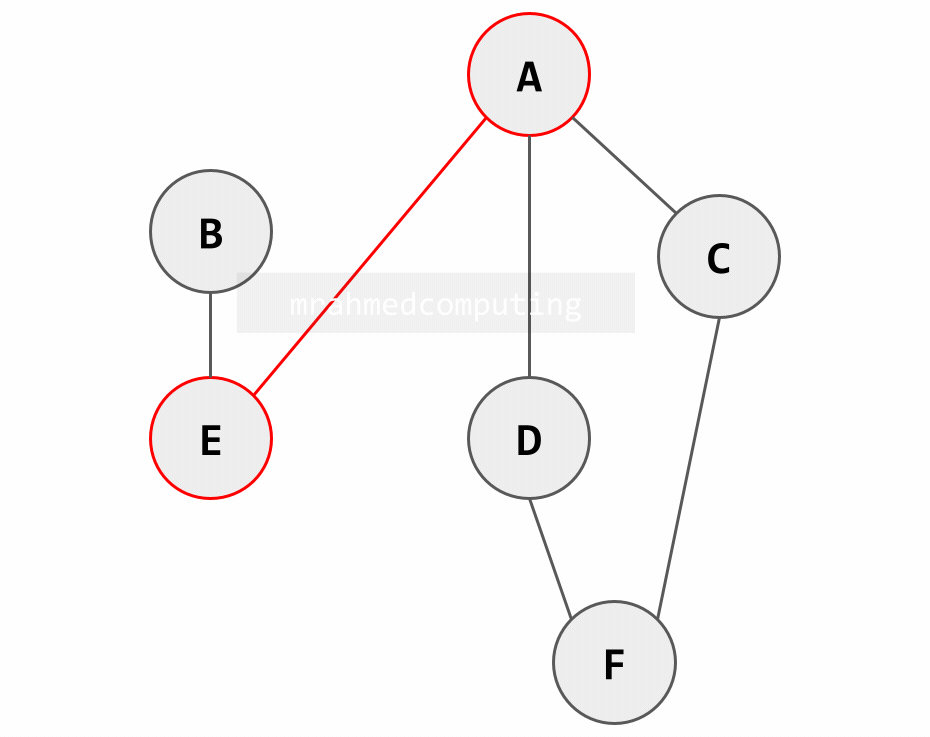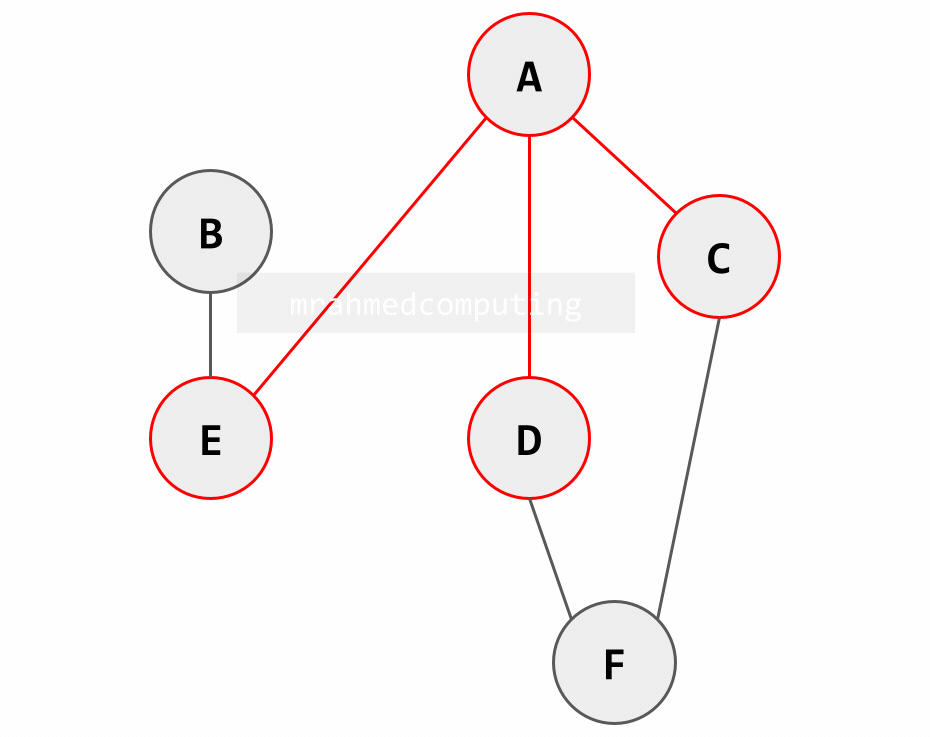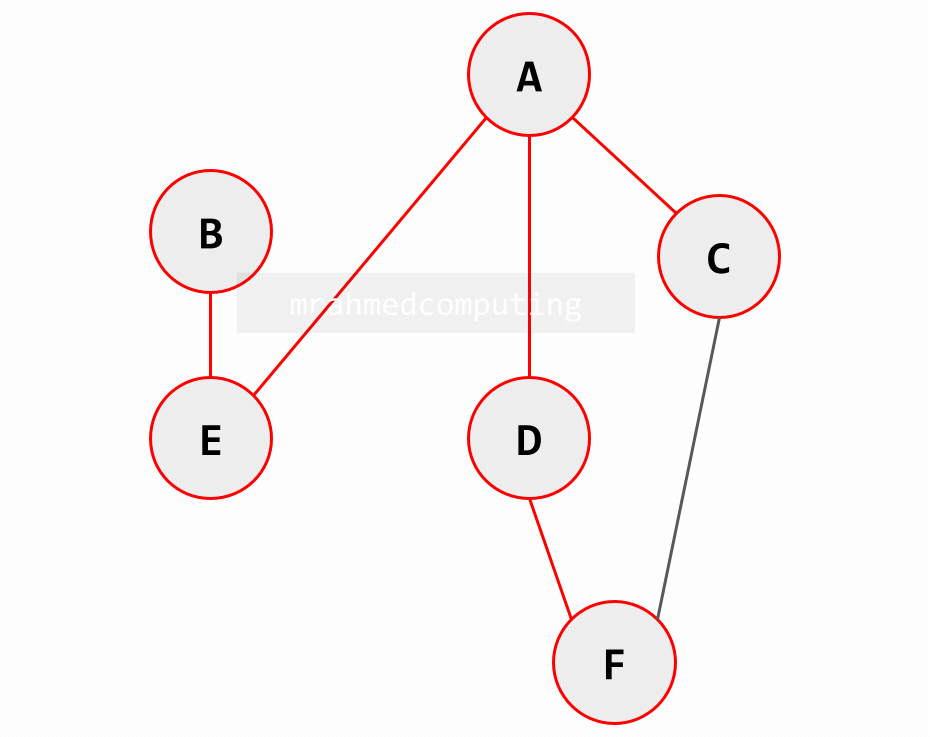
Depth-First Traversal

In this traversal, we go as far down one route as we can before backtracking and taking the next route. When given the chance we always start from the left.

Start from the left.

[A]
[A,E]
[A,E,B]
[A,E,B,F]
[A,E,B,F,D]
[A,E,B,F,D,C]

Note: Pay attention. Image to the right/below is animated.

Breadth-First Traversal

With a breadth-first traversal, we visit all the neighbours of a node, and then all the neighbours of the first node visited, then all the neighbours of the second node and so on, before moving further away from the start node.