Lesson 5. Trees
Lesson Objective
- Know that a tree is a connected, undirected graph with no cycles.
- Know that a binary tree is a rooted tree in which each node has at most two children.
- Be familiar with typical uses for rooted trees.
- Be able to trace recursive tree-traversal algorithms: pre-order, post-order, in-order
- Understand uses of different traversal outputs.
Lesson Notes
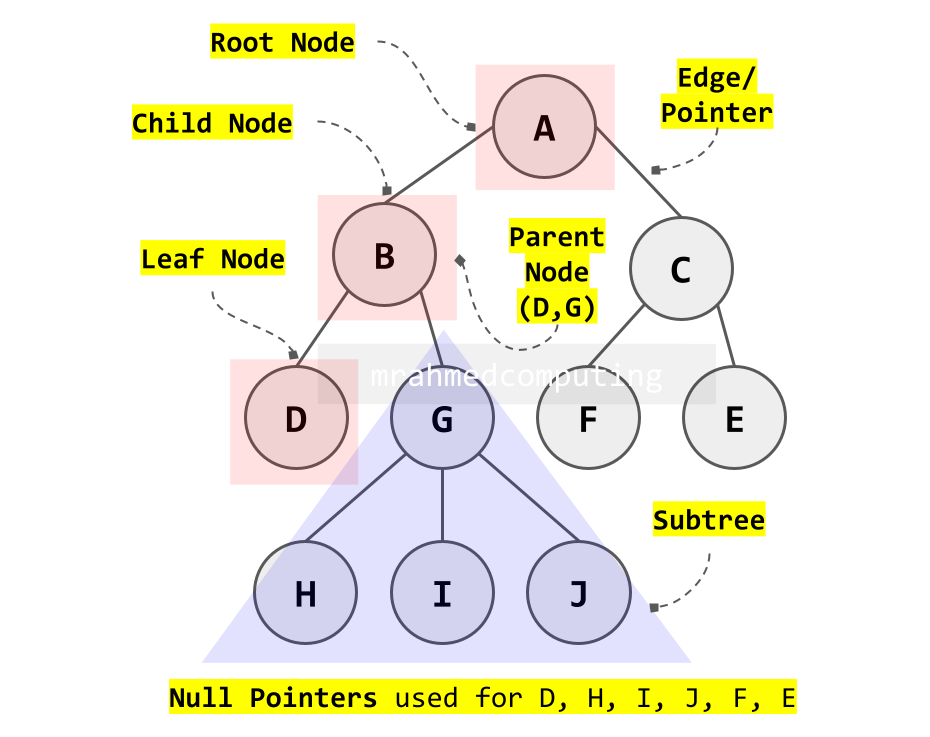
Tree Data Structures
A fundamental data structure used in many computing areas.
A tree is a connected, undirected graph with no cycles (i.e. there is a unique path from each node to any other node).
In a rooted tree, one node is identified as the root.
Every node except the root has one unique parent.
Binary Trees
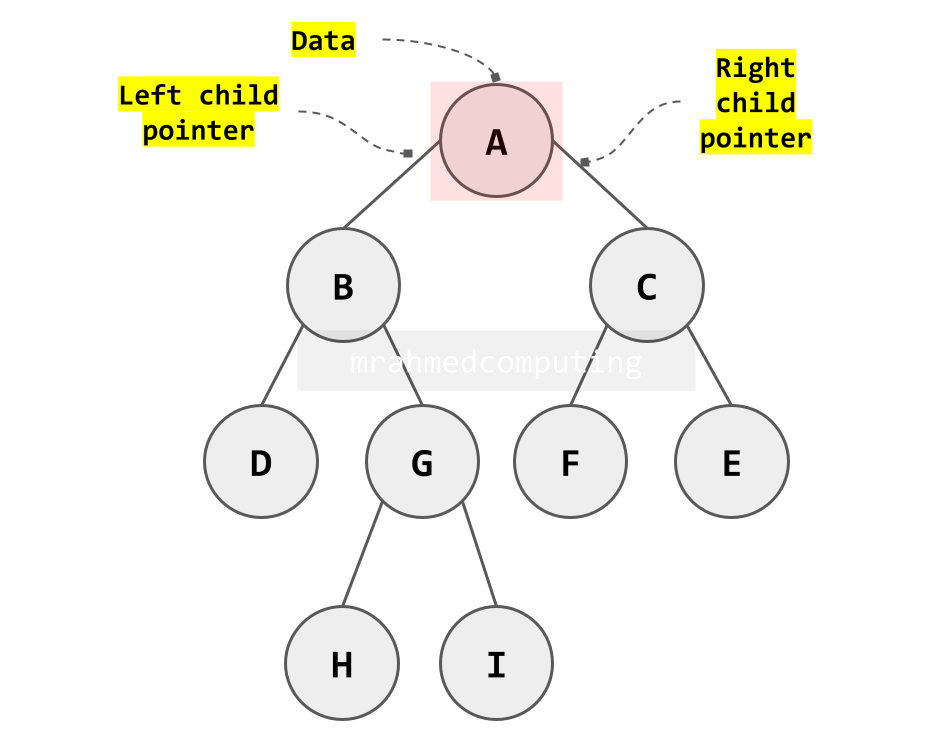
A binary tree is a rooted tree in which each node has a maximum of two children.
Each node consists of 3 parts:
- The data (which may be a primitive or more complex object).
- A left pointer to a child.
- A right pointer to a child.
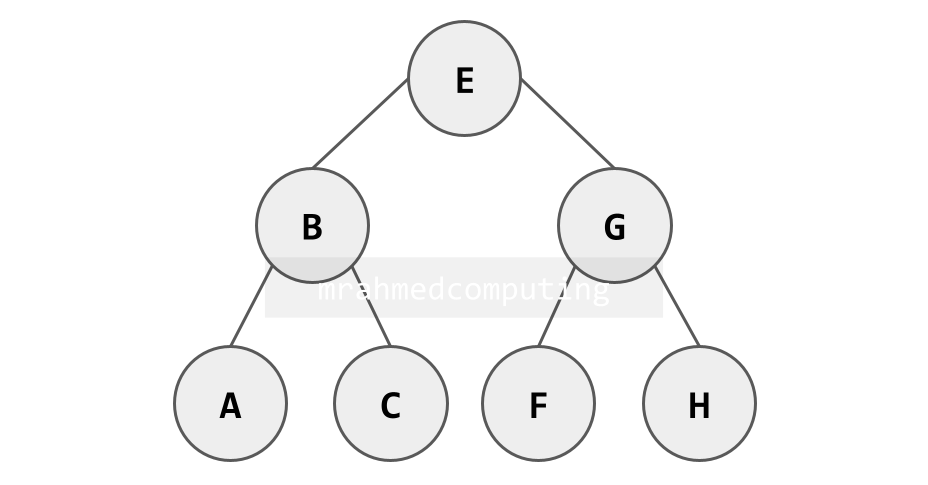
Binary Tree in Memory
Here is an example of a binary tree being represented as a dictionary of arrays.
Python Code:
BinaryTree = {“E”:[“B”,“G”],“B”:[“A”,“C”],“G”:[“F”,“H”],“A”:[],“C”:[],“F”:[],“H”:[]}
Linked List and Array Binary Tree Implementation
Tree Drawing:
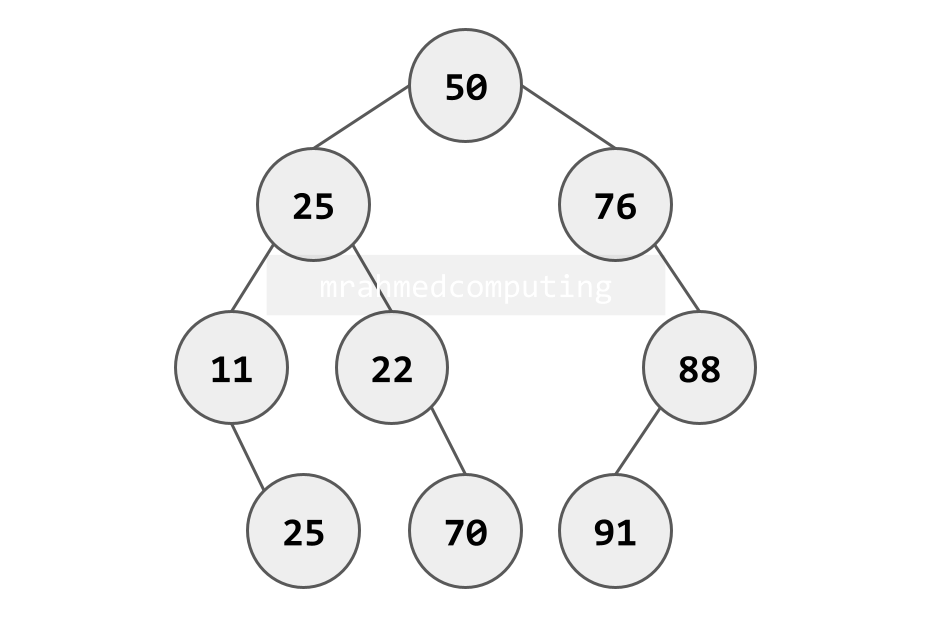
Here is another Binary Tree.
This binary tree will be used in the following linked list and array examples.
The root node of this tree contains the data value 50. There are a number of parent and child nodes.
Linked List Tree:
In the example below. The start memory location is 01. Each node is assigned a data value. The right and left pointers are assigned memory locations to point to other nodes in the tree.
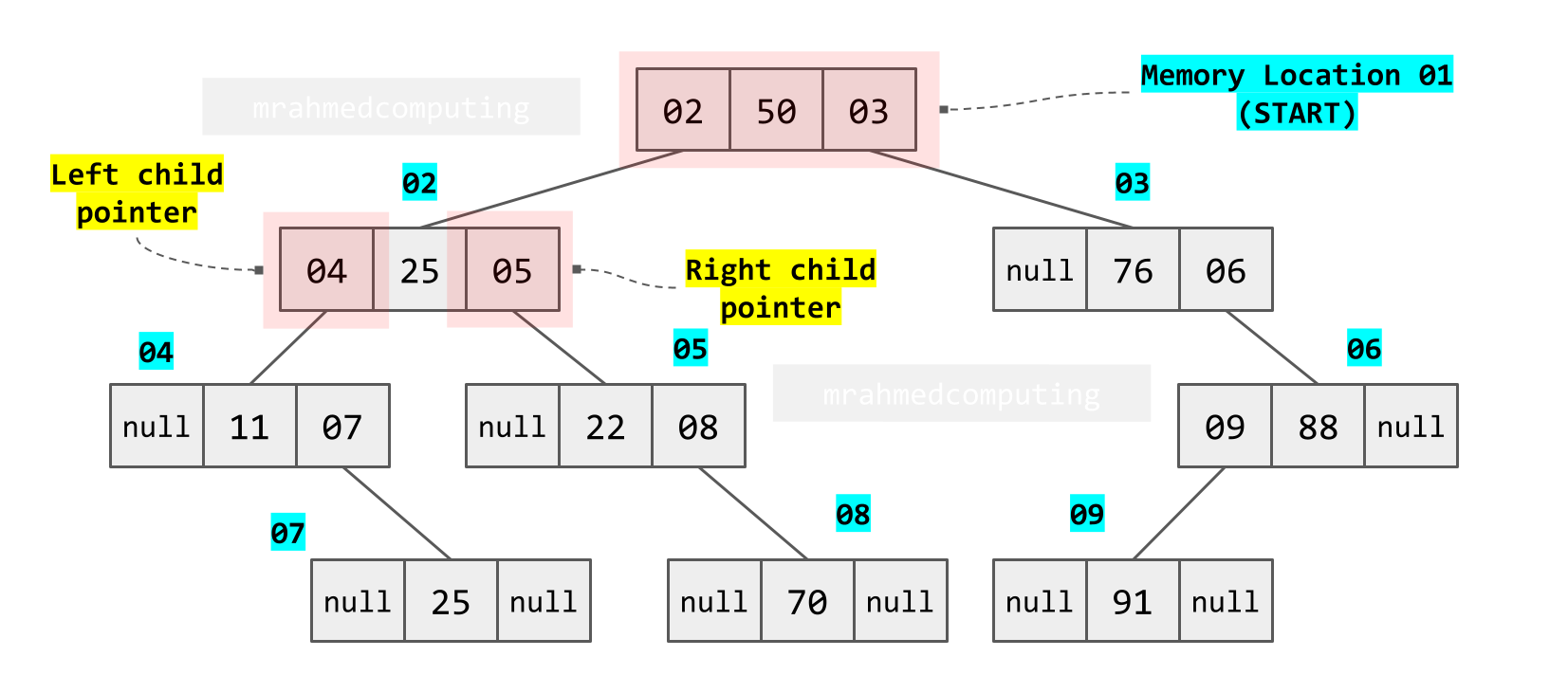
Array Binary Tree:

Left and right positions of a node are identified by using the following formula:
- Left = 2 * Parent
- Right = 2 * Parent + 1
Root location formula:
Note: Linked lists Memory Location don't apply to this.
| Parent |
Left C. |
Right C. |
| 01 |
02 |
03 |
| 02 |
04 |
05 |
| x |
2*X |
2*X+1 |
Tree Applications
Tree data structures are used in a wide variety of applications, including:
- File systems: Tree data structures are used to represent the hierarchical structure of files and directories in file systems. The directory structure on your computer is a tree data structure, with files and subdirectories represented as nodes in the tree.
- Databases: Tree data structures are used to index data in databases, which can improve the efficiency of search and retrieval operations.
- Routers: Tree data structures are used to store routing information in routers, which allows them to efficiently route packets to their destinations. Wireless and wired networks.
- Decision making: Tree data structures can be used to represent decision trees, which are used in artificial intelligence and machine learning to make decisions.
- Sorting and searching: Tree data structures can be used to implement efficient sorting and searching algorithms.
- Compression algorithms: Huffman Coding?
Here are some specific examples of how tree data structures are used in real-world applications:
- The search bar on a website: When you use the search bar on a website, the website's server uses a tree data structure to index the website's content. This allows the server to quickly find the pages that are most relevant to your search query.
- The autocomplete feature on a smartphone: The autocomplete feature on your smartphone uses a tree data structure to store a dictionary of words. This allows the phone to suggest words as you type, which can help you to type more quickly and accurately.
- The spam filter in your email inbox: Your email inbox's spam filter uses a tree data structure to classify emails as spam or not spam. This helps to keep your inbox free of unwanted emails.
- The recommendation engine on a streaming service: The recommendation engine on a streaming service uses a tree data structure to store information about your viewing habits. This allows the service to recommend new shows and movies that you are likely to enjoy.
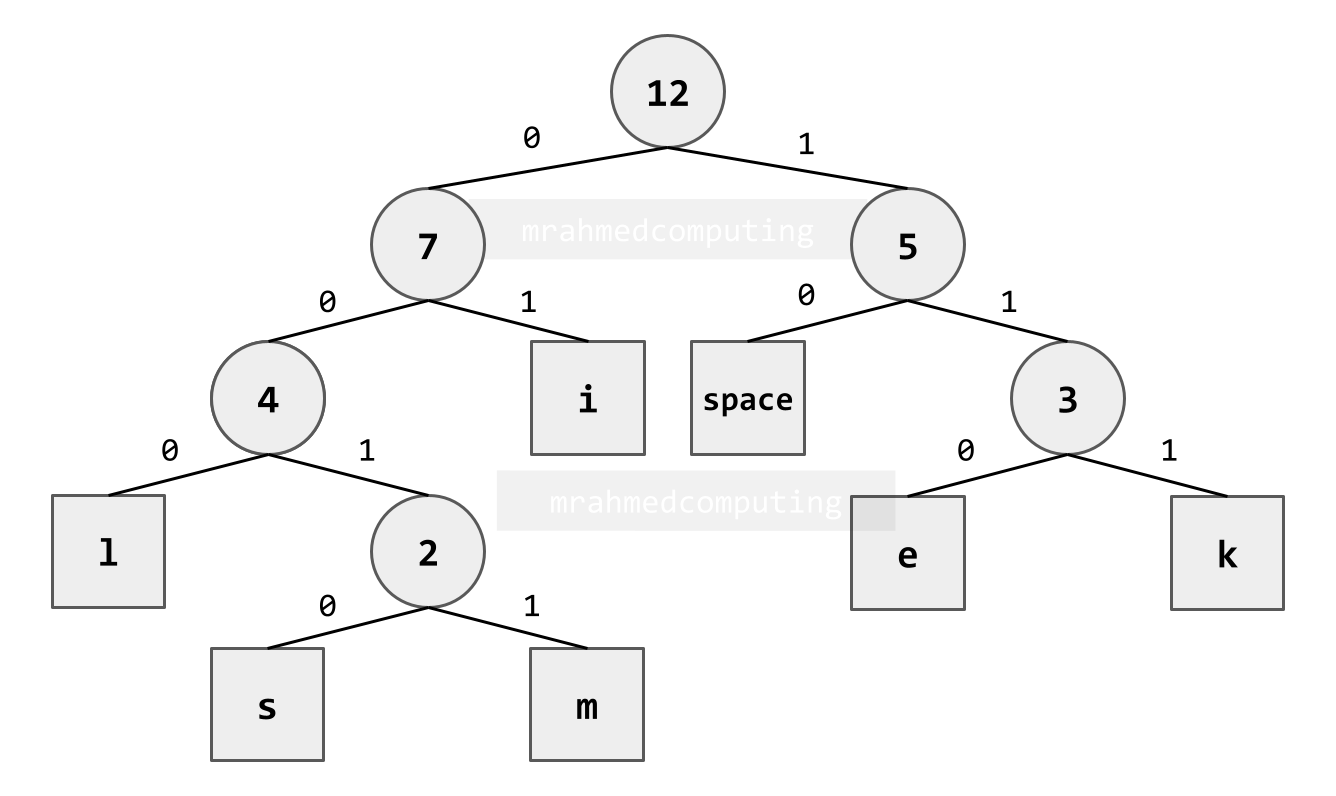
Tree Application: Huffman Coding
Text to Compress:
i like limes (7 bit ASCII)
12 x 7 = 84 bits (original file size)
Compression Process:
- i = 3 chars x 2 bits = 6 bits
- space = 2 chars x 2 bits = 4 bits
- l = 2 chars x 3 bits = 6 bits
- k = 1 char x 3 bits = 3 bits
- e = 2 chars x 3 bits = 6 bits
- m = 1 char x 4 bits = 4 bits
- s = 1 char x 4 bits = 4 bits
6 + 4 + 6 + 3 + 6 + 4 + 4 = 33 bits (compressed file size)
84 bits - 33 bits = 51 bits saved
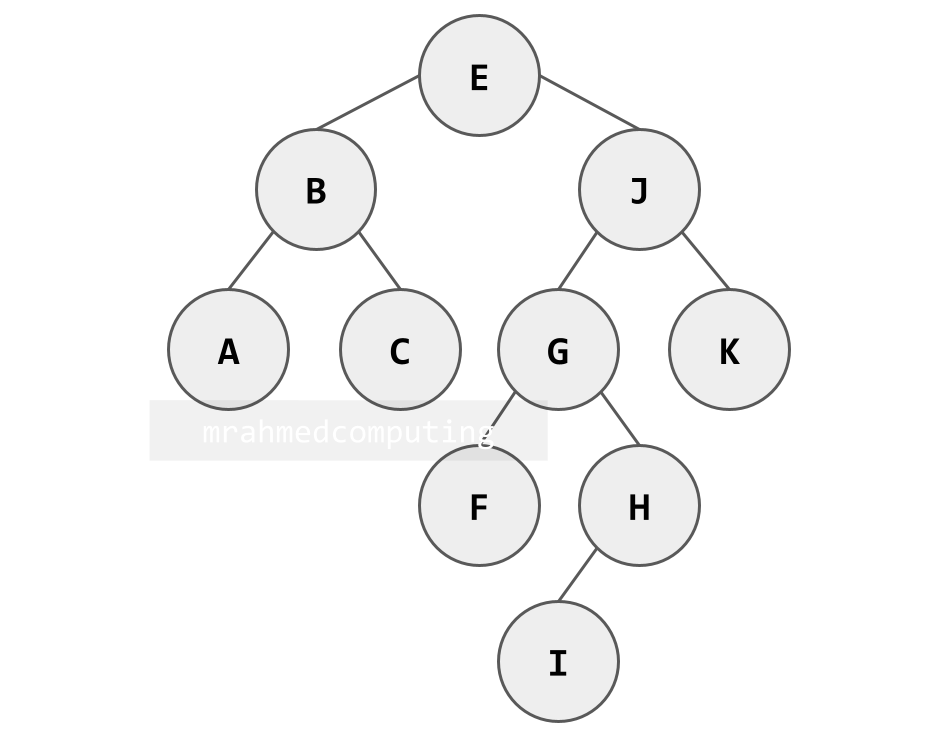
Binary Search Tree
When building a binary search tree, nodes are added in the order given, with the first item at the root.
Starting at the root each time, if the next item is less than the root, it is added to the left of the root, otherwise, to the right.
Apply the same rule at the root of each sub-tree.
[E, B, J, A, G, H, C, I, F, K]
When searching a binary search tree, nodes must follow the criteria.
- Must be a binary tree.
- No value can is repeated.
- Any values left of a root will be less than the root and values on the right will be more than the root.
Example:
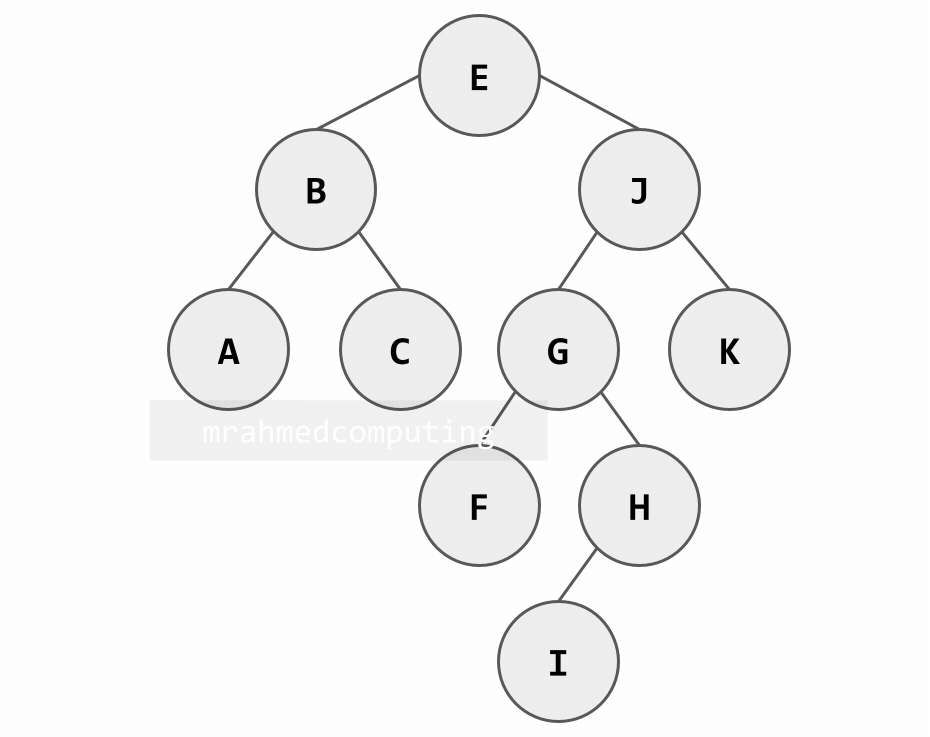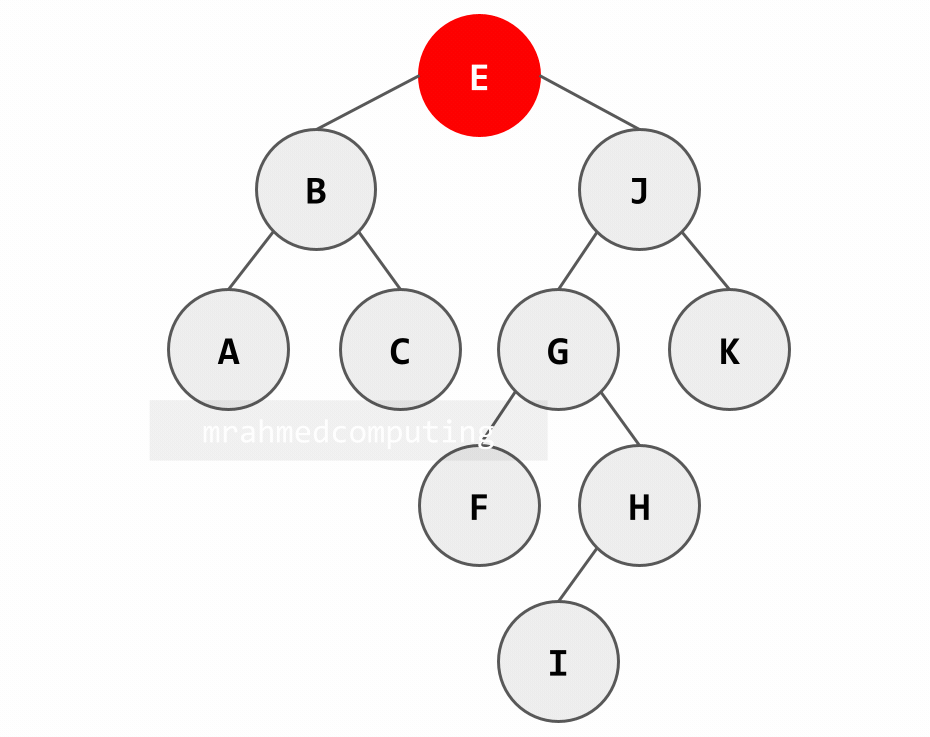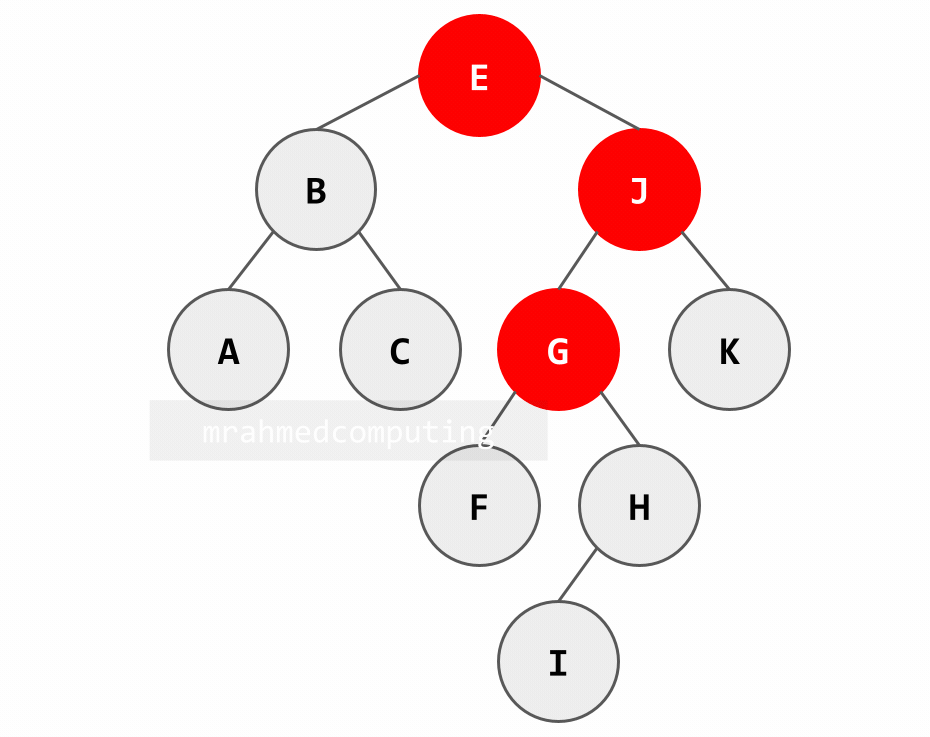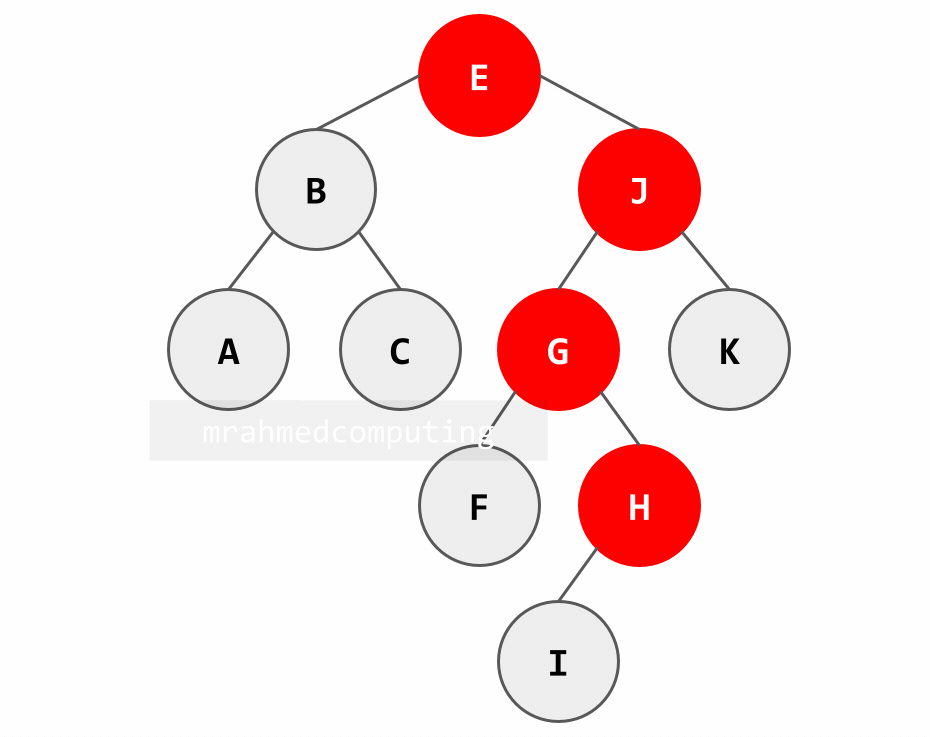
Apply the binary search logic. When searching for H:
- H = E (H > E)
- H = J (H < J)
- H = G (H > G)
- H = H (H = H)
Note: Image on the right/bottom is animated and shows the different stages of the search.
Binary Tree Traversal
A binary tree can be traversed in three different ways:
- Pre-order Traversal: Visit the root, then traverse the left sub-tree, then the right sub-tree.
- In-order Traversal: Traverse the left sub-tree, then visit the root, then traverse the right sub-tree.
- Post-order Traversal: traverse the left sub-tree, then traverse the right sub-tree, then visit the root.
Pre-order Traversal:
- Process the root (R).
- Traverse the left-subtree of R in pre-order.
- Traverse the right-subtree of R in pre-order.
[E, B, A, C, J, G, F, H, I, K]
Note: Image on the right/bottom is animated and shows the different stages of the search.
Pre-order Traversal Example:
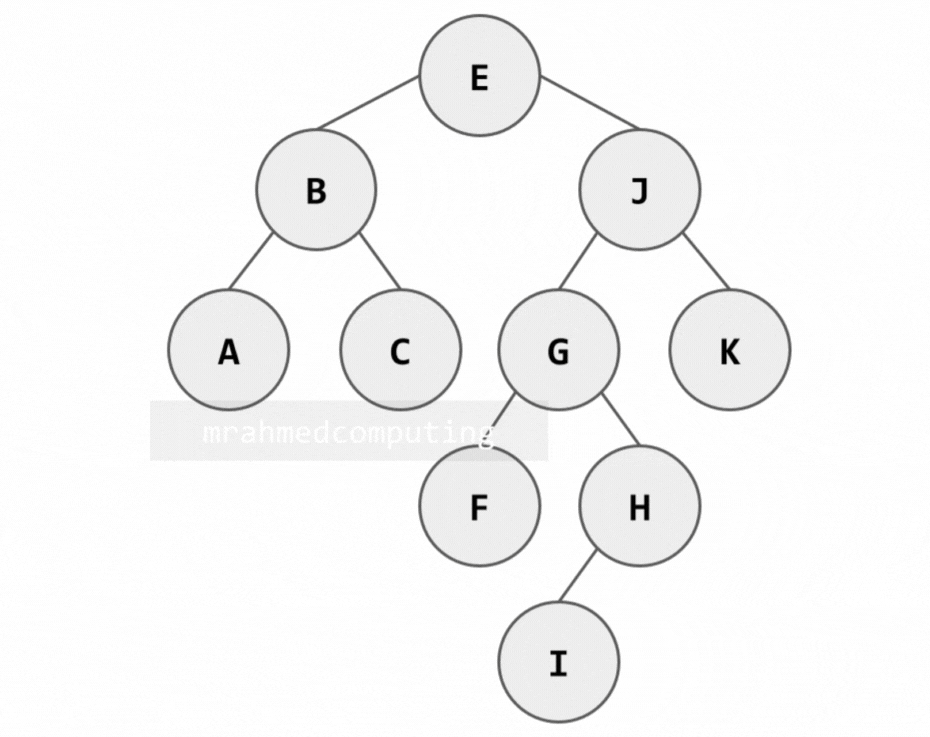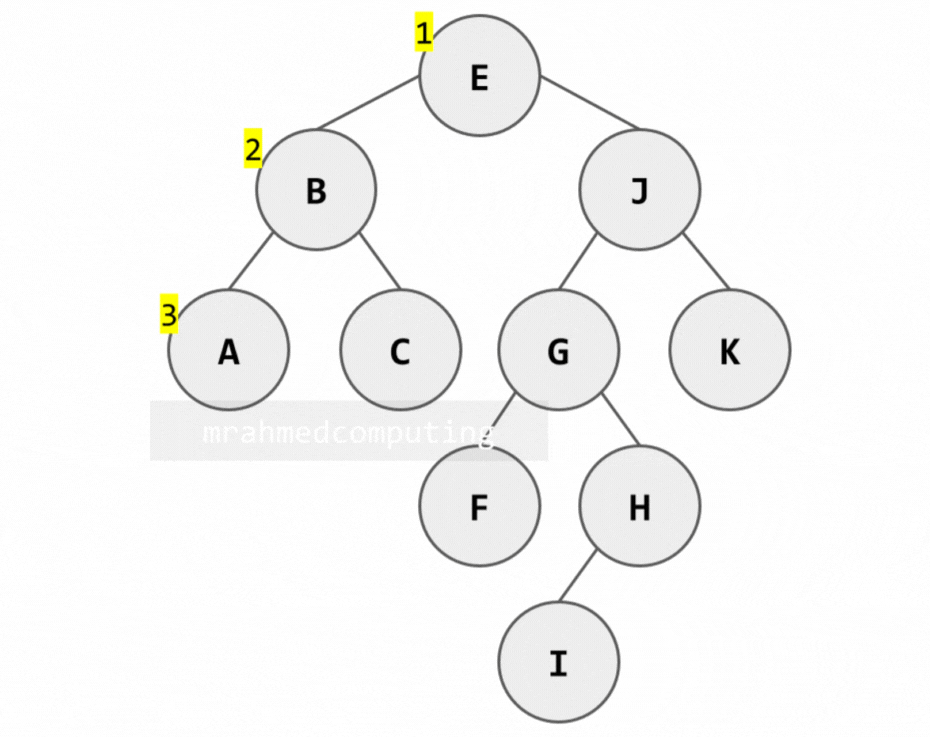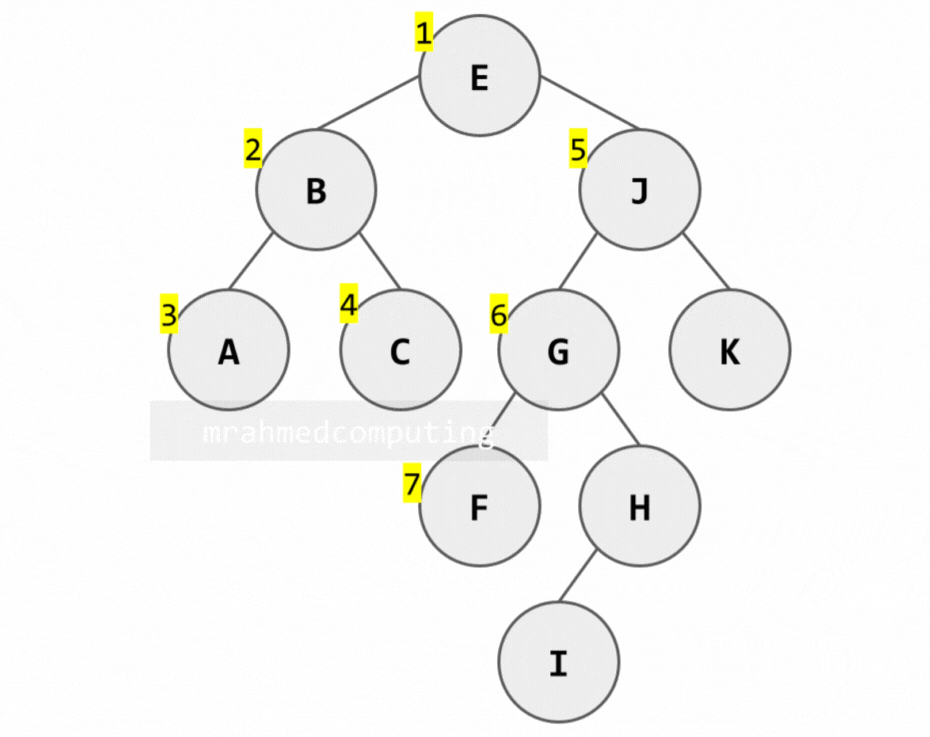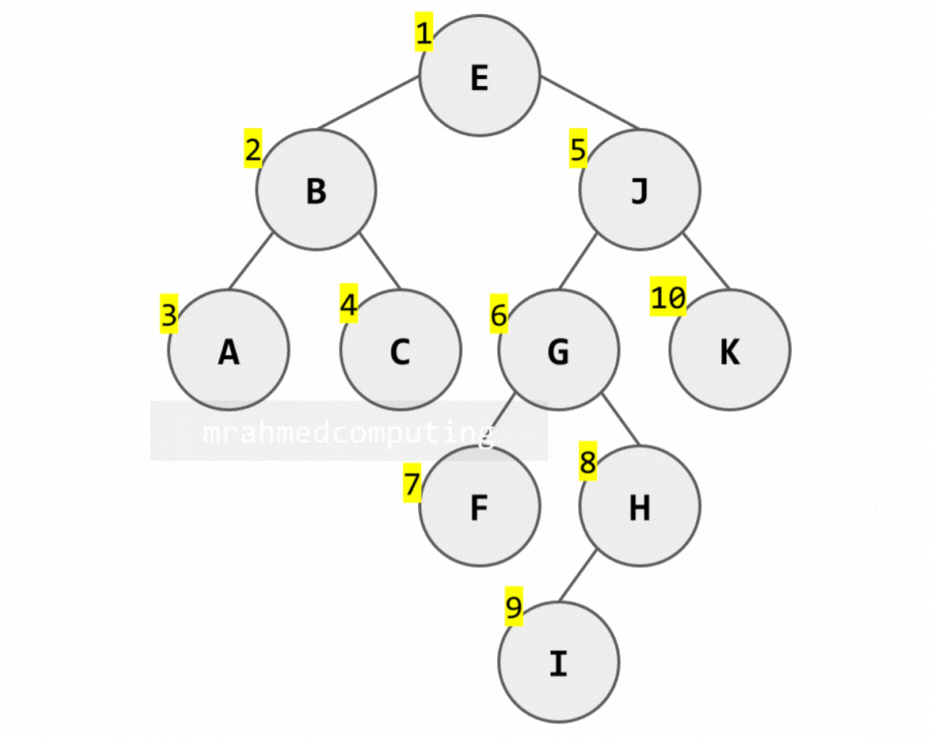
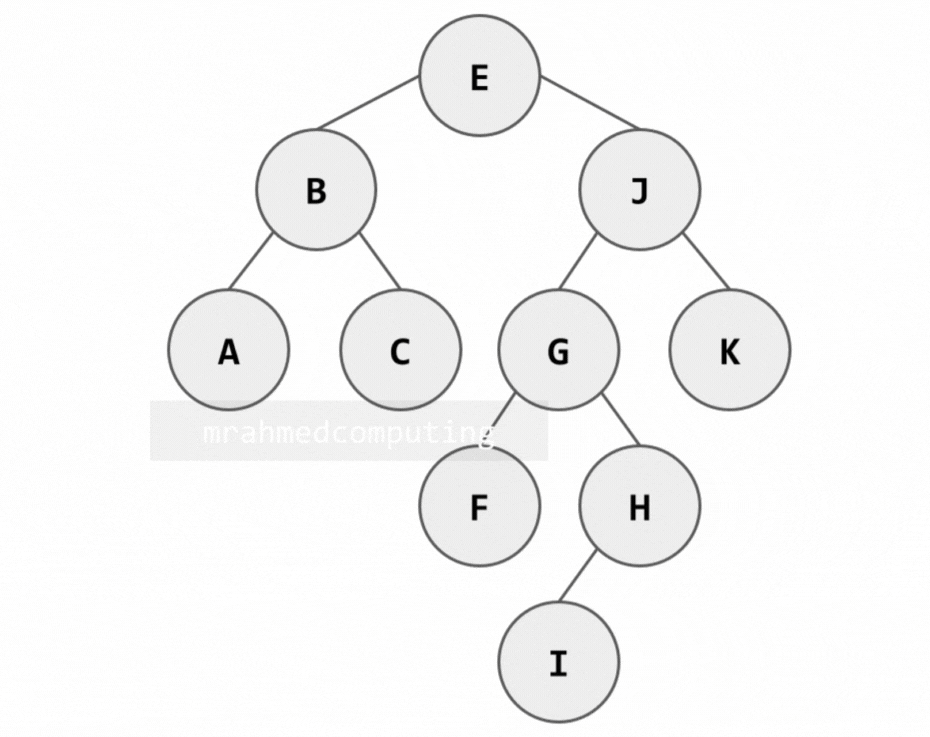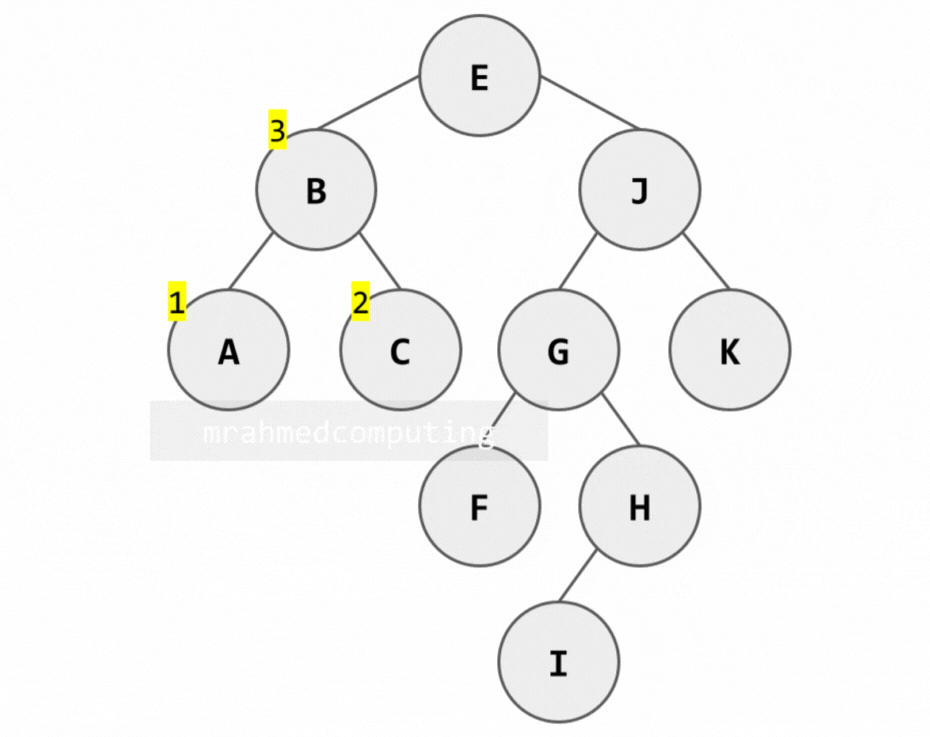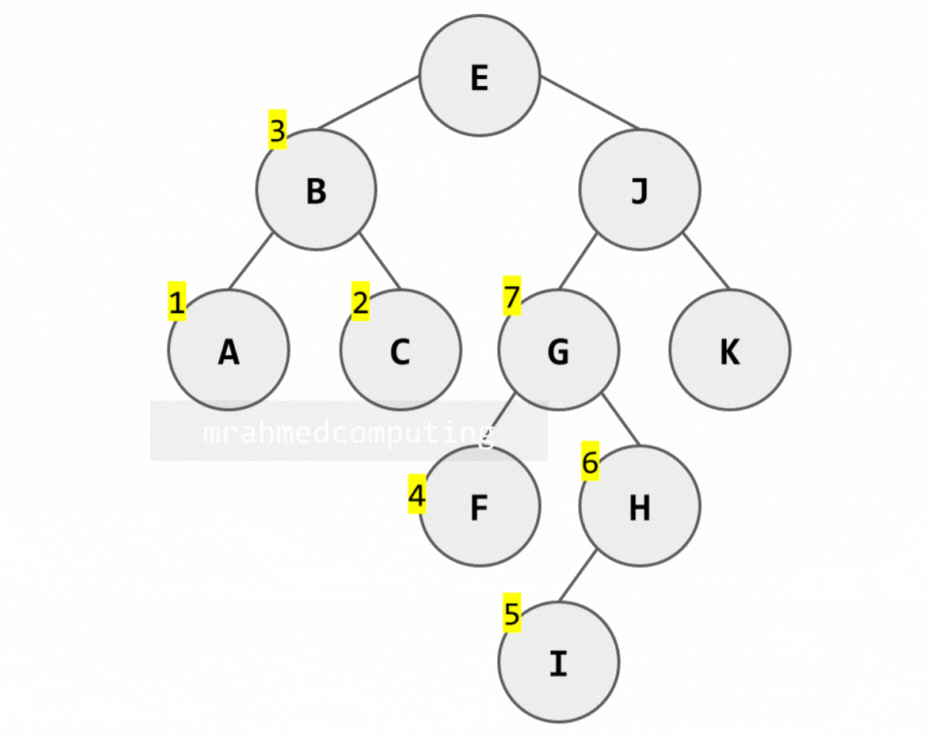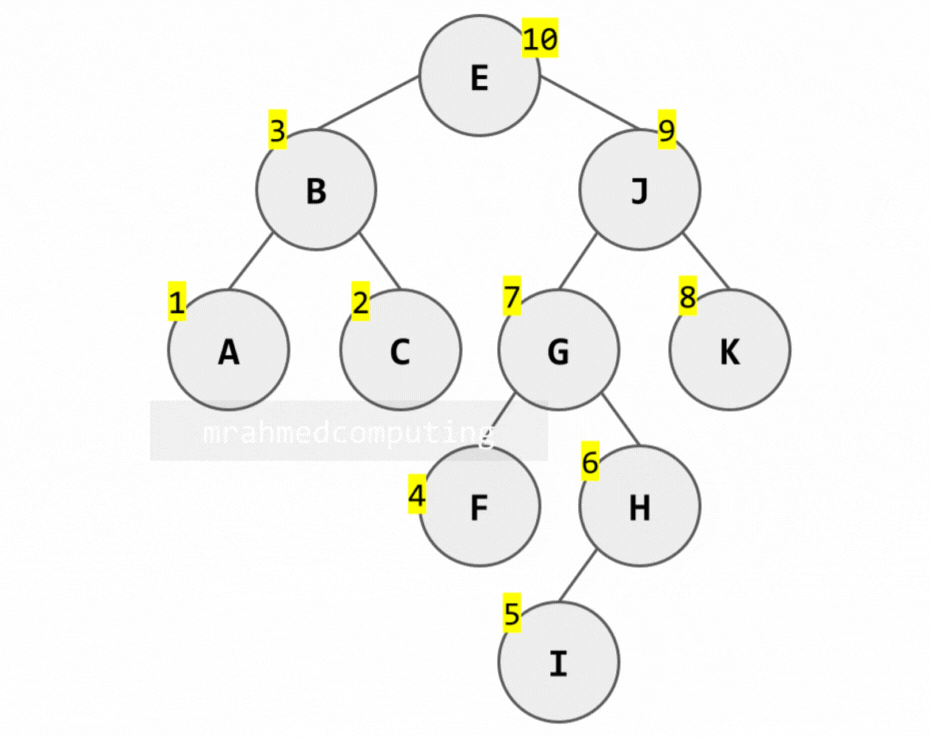
In-order Traversal:
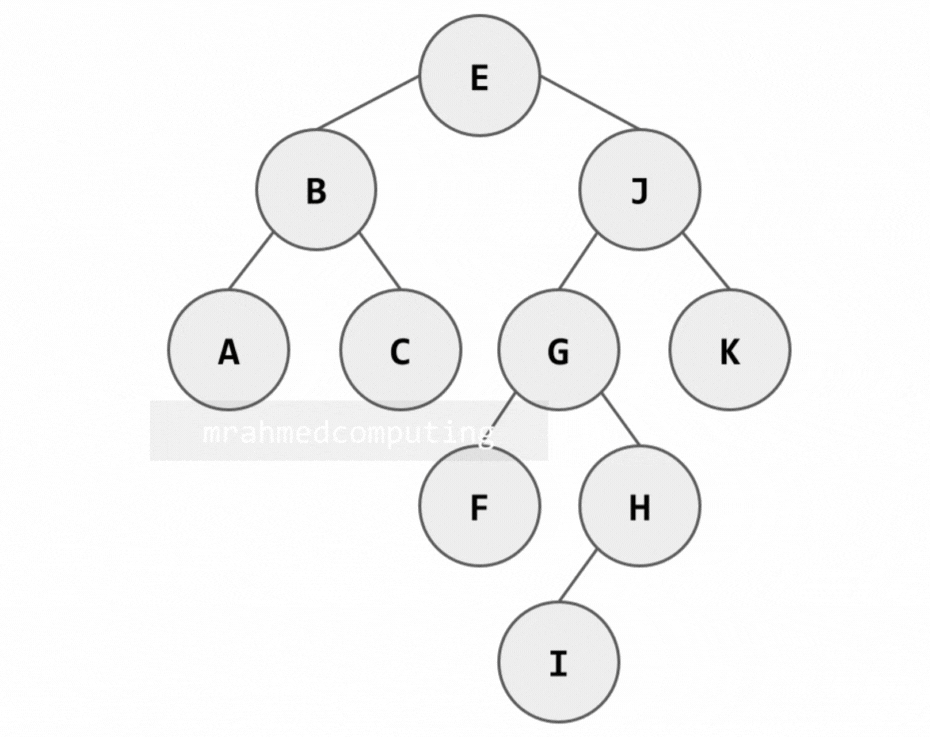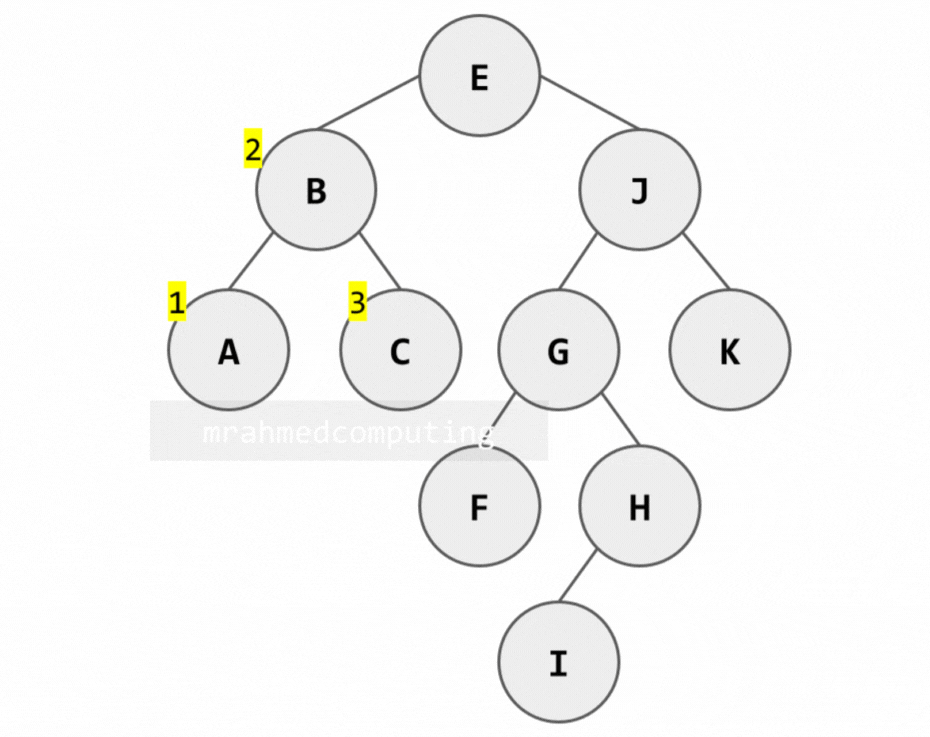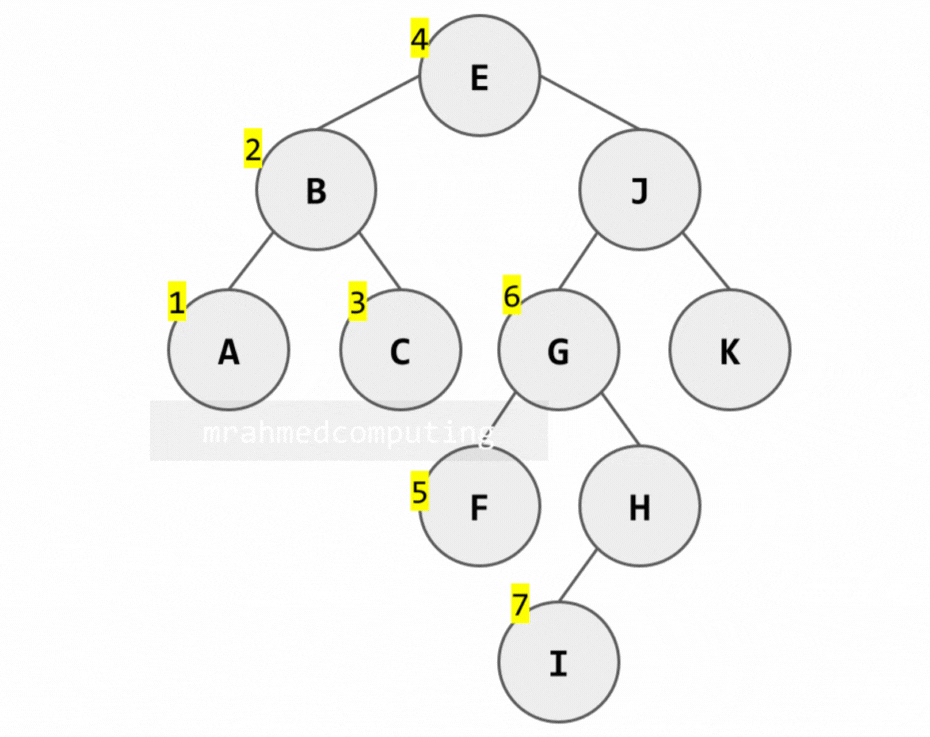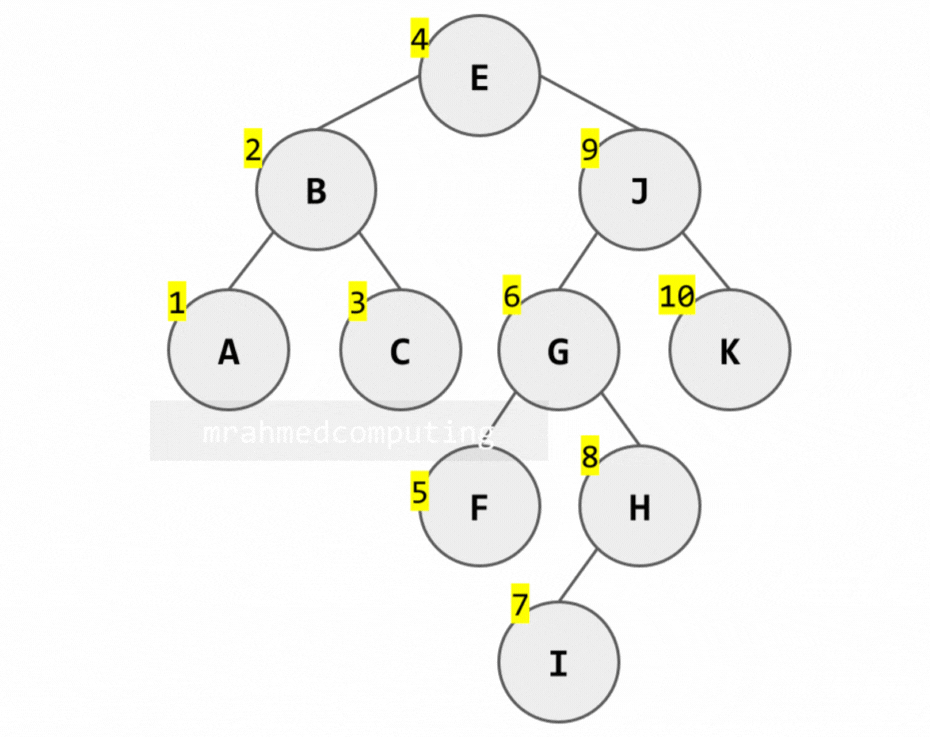
- Travers the left-subtree of the Root (R).
- Process the Root (R).
- Traverse the right-subtree of R in inorder.
[A, B, C, E, F, G, I, H, J, K]
Note: Image on the right/bottom is animated and shows the different stages of the search.
In-order Traversal Example:
Post-order Traversal:
- Traverse the left-subtree of the Root (R).
- Traverse the right-subtree of the Root (R).
- Process the Root (R).
[A, C, B, F, I, H, G, K, J, E]
Note: Image on the right/bottom is animated and shows the different stages of the search.
Post-order Traversal Example:
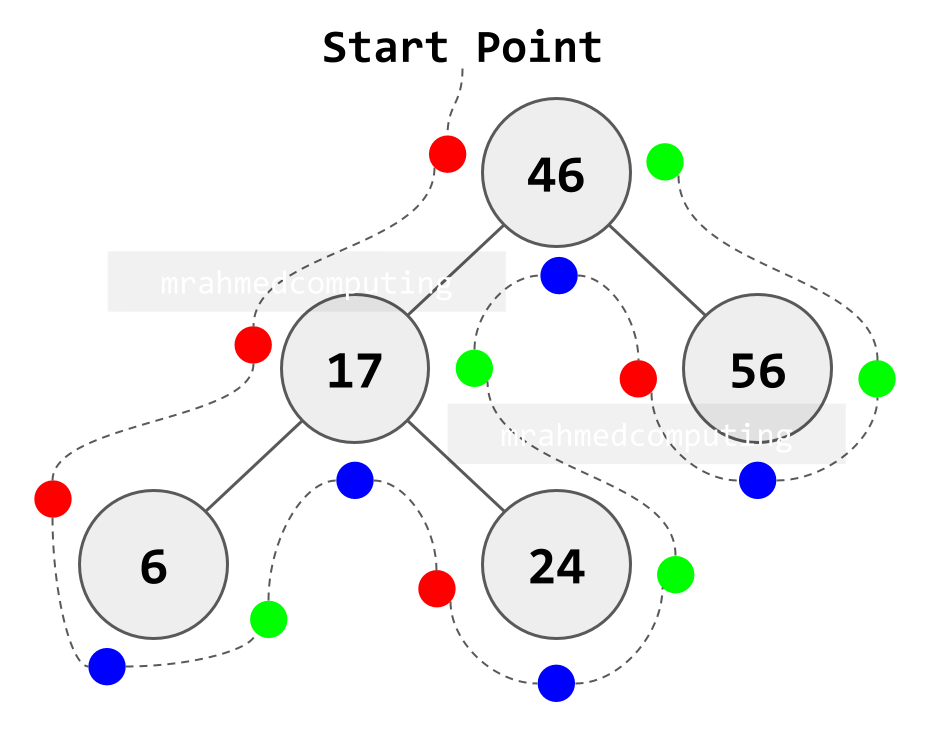
Binary Tree Traversal - Summary
This diagram shows which node to examine in order depending on the traversal being used. You start from the top left of the root node. If you are using Pre-order traversal, you examine the node when you pass from the left. If you are using In-order traversal, you examine the node when you pass the bottom of the node. If you are using Post-order traversal, you examine the node when you pass the right side of the node.
- Pre-order - Left of Node
- In-order - Bottom of Node
- Post-order - Right of Node
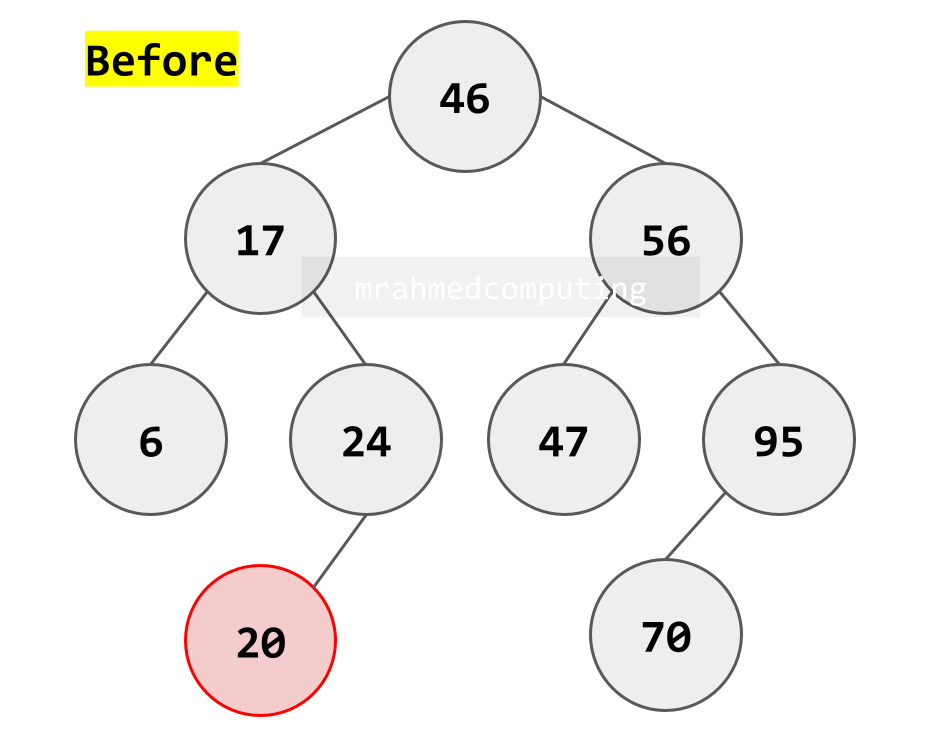
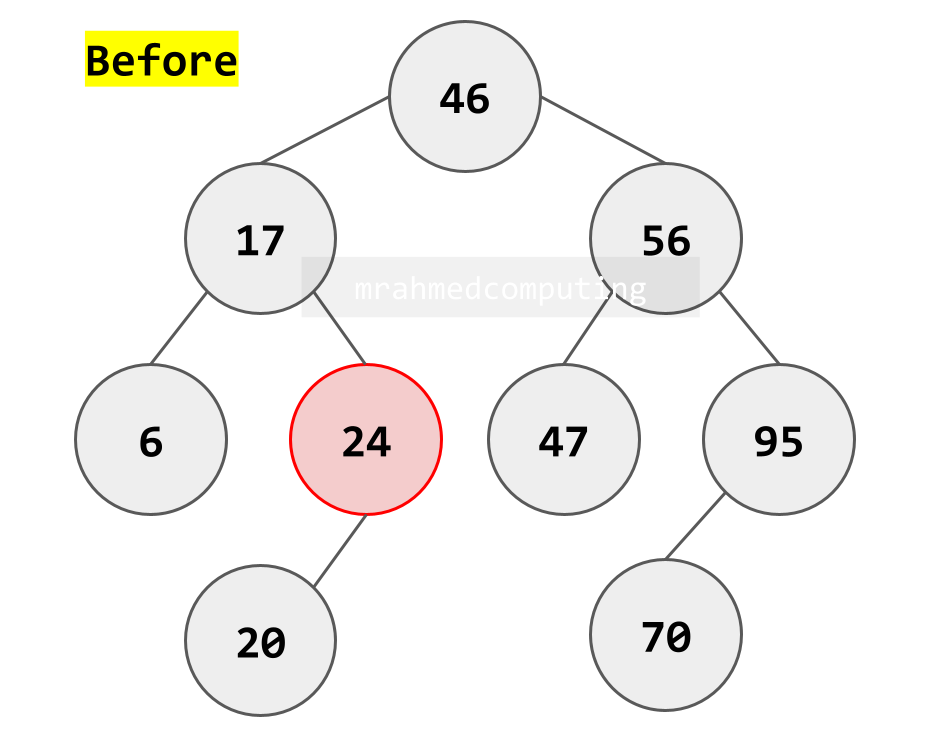
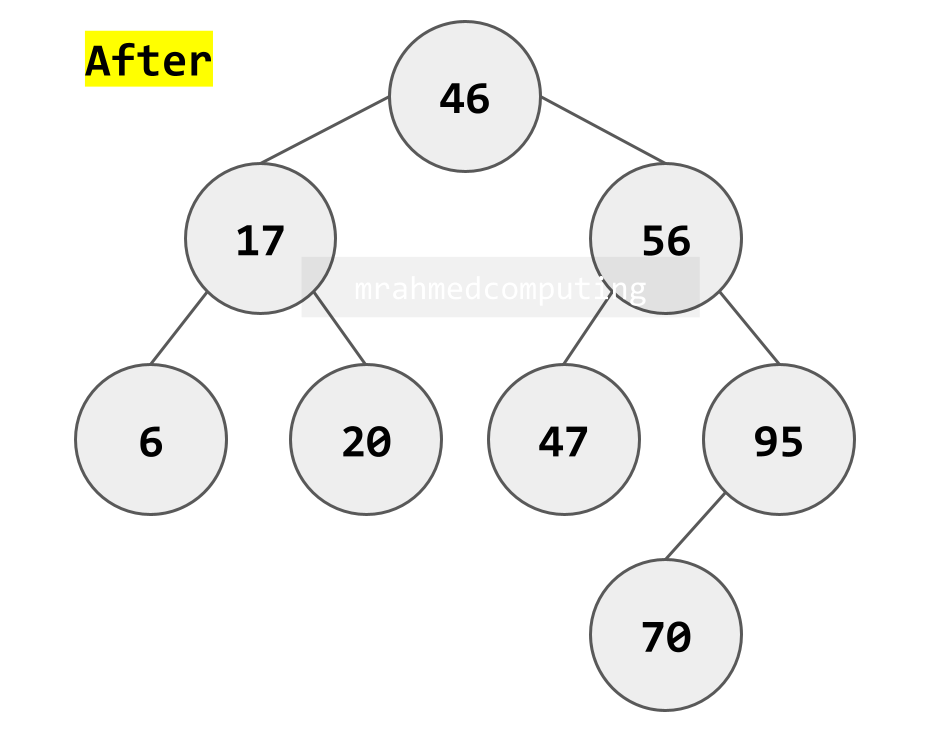
Deleting a Node
There are three separate cases to consider:
- The node to be deleted is a leaf node (has no children)
- The node to be deleted has only one child
- The node to be deleted has two children
Example: The node to be deleted has no children
Example: The node to be deleted has one child
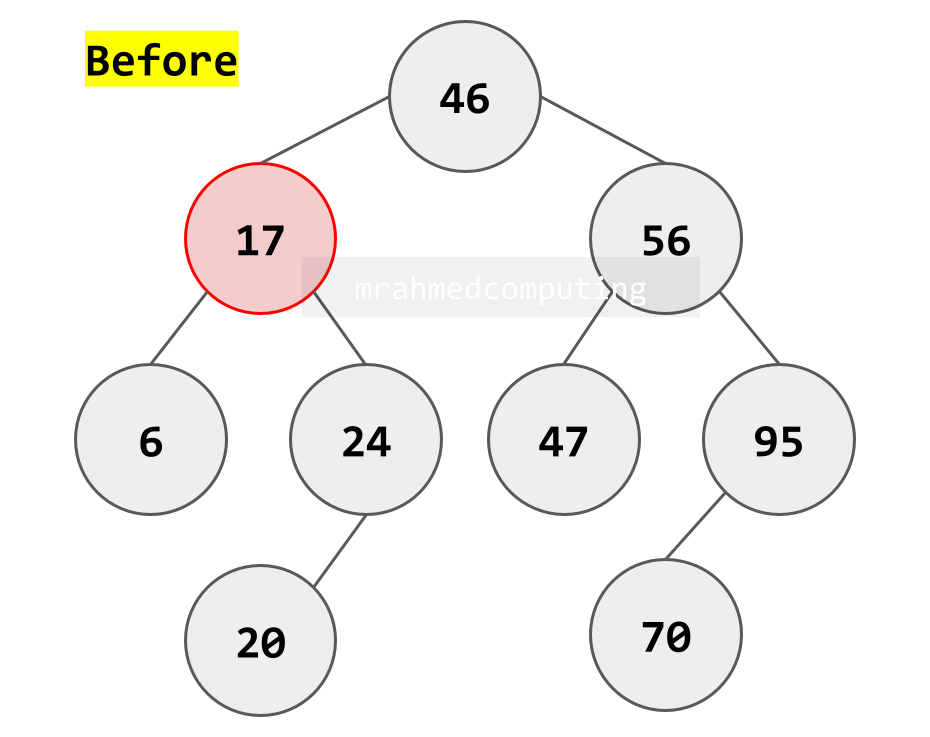
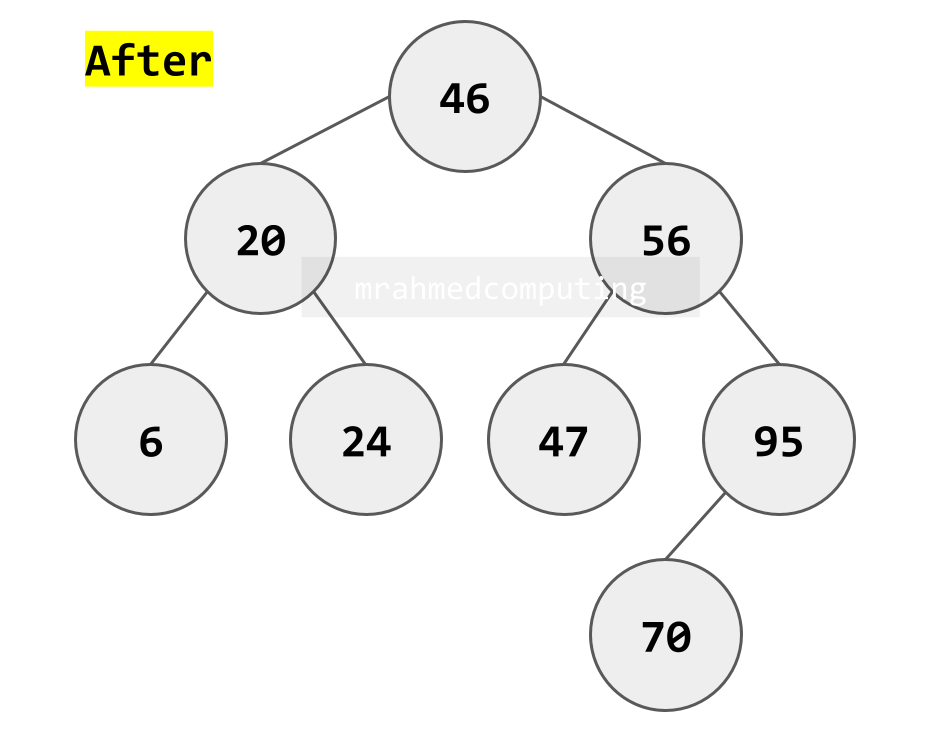
Example: The node to be deleted has two children
Note: Find a node that will preserve the search tree properties, and put it in the place of the deleted node. This will be the node that has the next-largest key.