Lesson 3. Karnaugh Maps
Lesson Objective
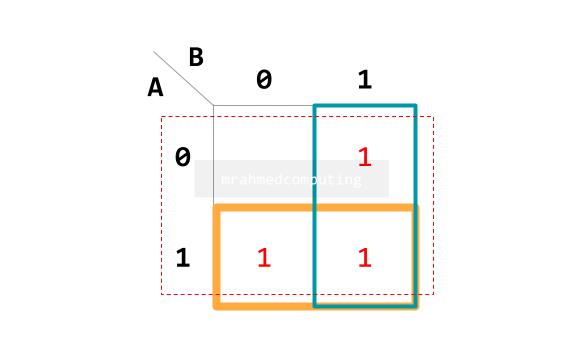
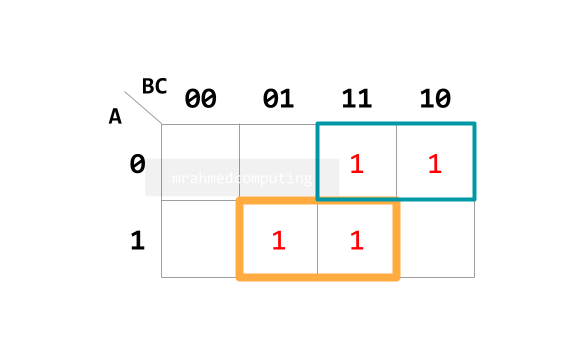
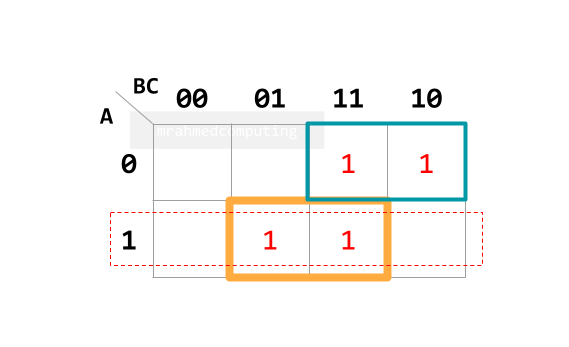
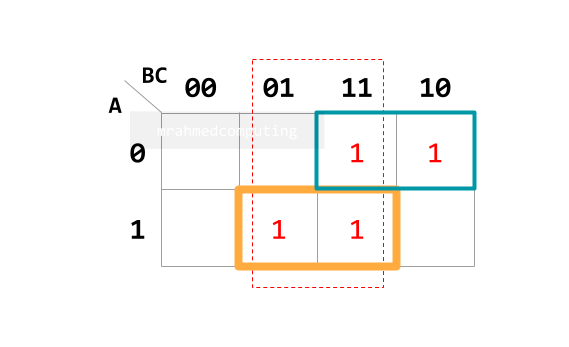
- Understand the correspondence between a truth table and a Karnaugh map.
- Understand how to fill out a Karnaugh map for a given expression.
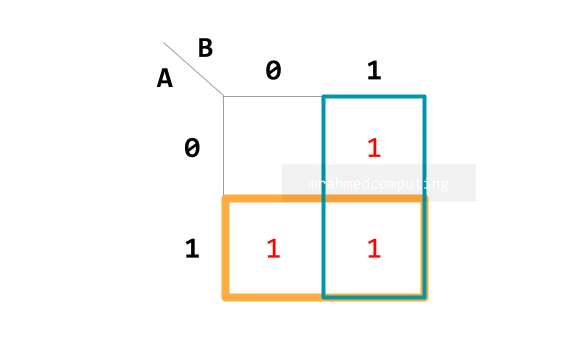
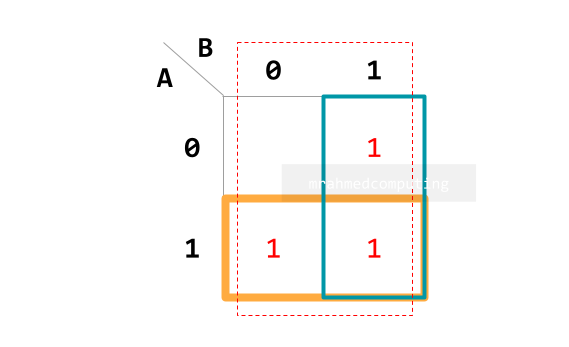
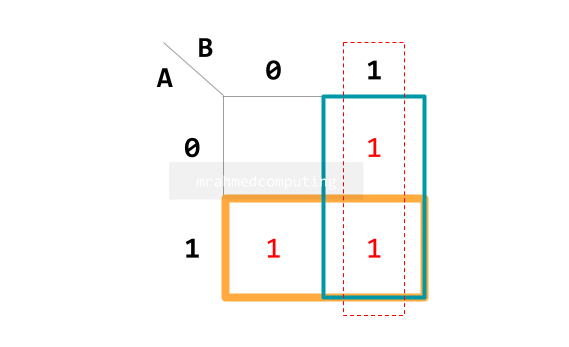
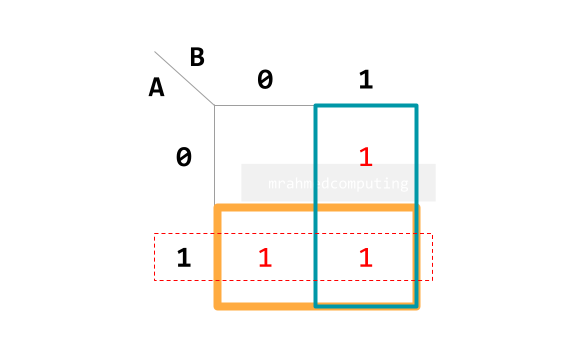
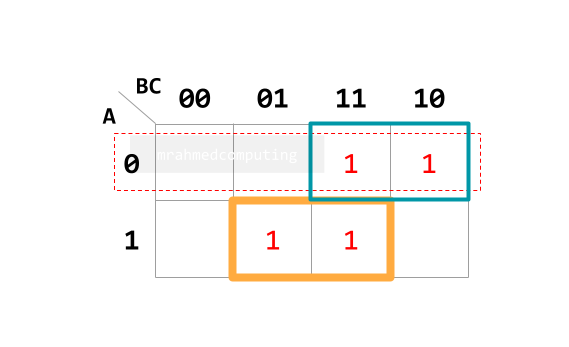
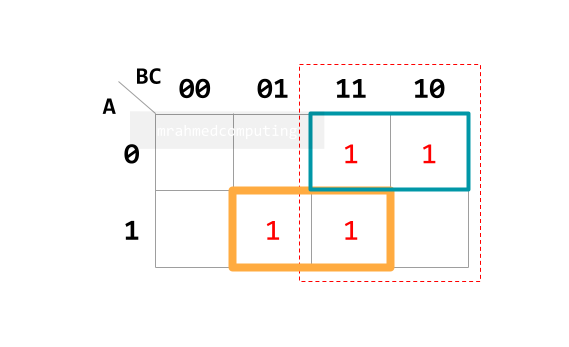
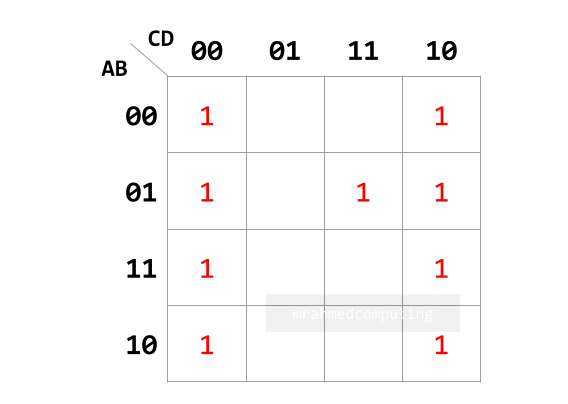
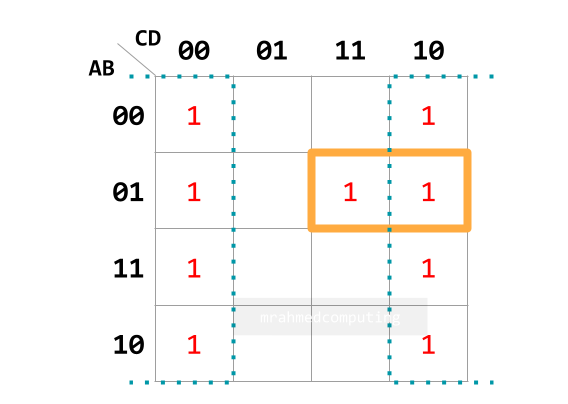
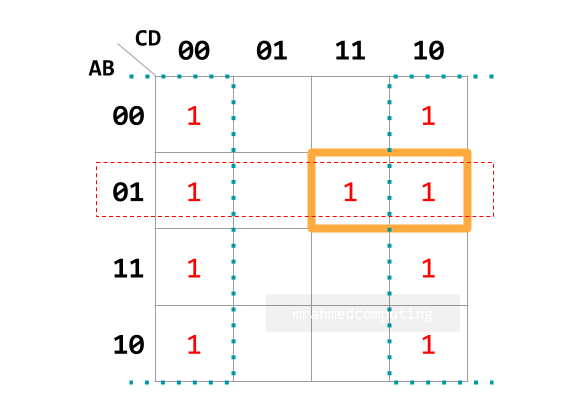
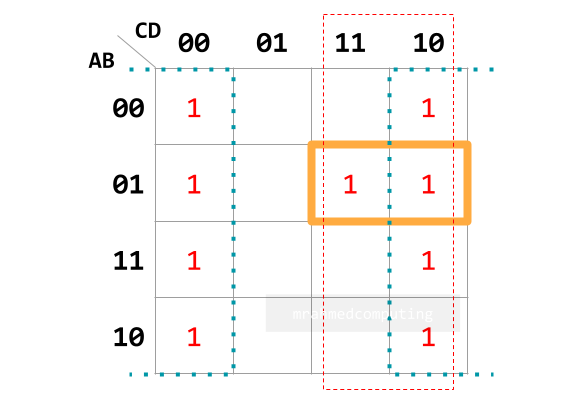
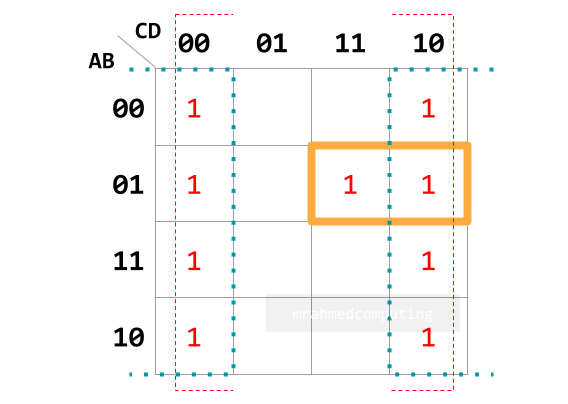
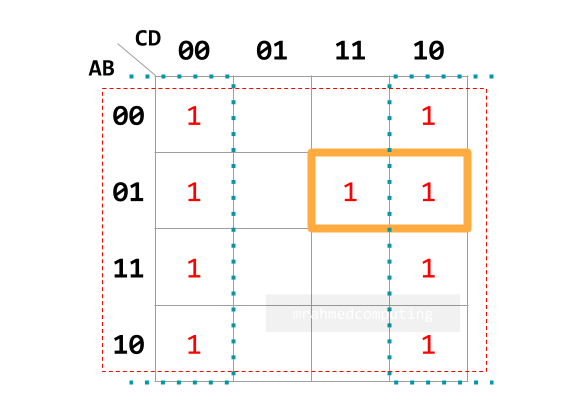
- Understand how to group items in a Karnaugh map.
- Interpret the groupings in a Karnaugh map.
- Simplify Boolean expressions with two, three or four variables using a Karnaugh map.
Lesson Notes
Boolean Algebra?
Boolean algebra is a mathematical system for working with logical values (true and false) and the operations that combine them. It's a formal method used to manipulate and simplify logical statements, which is very important in computer science and digital circuit design. Rules for simplifying Boolean expressions, like absorption (X ⋀ (X ⋁ Y) = X) and general (X ⋁ ¬X = 1), help us reduce complex expressions to simpler forms that are easier to understand and use.
De Morgan's laws are a key tool for handling negations of combined terms. Specifically, they state that the opposite of "A or B" is the same as "not A and not B," and the opposite of "A and B" is the same as "not A or not B." These laws are crucial for simplifying and changing Boolean expressions, which often results in more efficient ways of implementing them.